Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo de Volumes – Discos e Anéis

Ver Teoria
Exercício 631234567891011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere a região R limitada pelas curvas de equações dadas. Aplicando o método dos discos circulares, calcule o volume do sólido obtido pela rotação da região R em torno do eixo E dado:

R :                     y = x 2 - 2 x ,   y = 4 - x ² E :                                                                       r e t a   y = 4

Passo 1

O lance é esboçar o mais precisamente possível os gráficos das funções pra entender bem a região R :

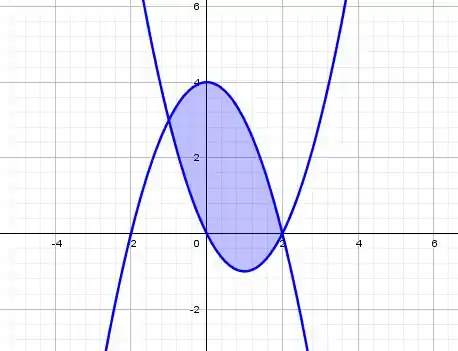
Passo 2

Então R é a área azul, cujos pontos de interseção vamos descobrir fazendo:

x 2 - 2 x = 4 - x 2 → x 2 - x - 2 = 0

x 1 = - 1     e   x 2 = 2

Então, temos - 1 ≤ x ≤ 2 .

Perceba que teremos que integrar em x , pois iremos girar em torno da reta y = 4 .

Assim, o método dos discos fica com a cara:

V = ∫ x 1 x 2 π f x - E 2 = ∫ x 1 x 2 π f x - 4 2

E o volume do sólido todo é:

∫ - 1 2 π x 2 - 2 x - 4 2 - 4 - x 2 - 4 2 d x = ∫ - 1 2 π - - x 2 2 + x 2 - 2 x - 4 2 d x

∫ - 1 2 π - x 4 + x 4 - 4 x 3 - 4 x 2 + 16 x + 16 d x = ∫ - 1 2 π - 4 x 3 - 4 x 2 + 16 x + 16 d x

∫ - 1 2 π - 4 x 3 - 4 x 2 + 16 x + 16 d x = π - x 4 - 4 3 x 3 + 8 x 2 + 16 x - 1 2 = 45 π

Resposta

∫ - 1 2 π x 2 - 2 x - 4 2 - 4 - x 2 - 4 2 d x = 45 π

Exercícios de Livros Relacionados

Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .