Em cada um dos exercícios a considere a região limitada pelas curvas de equações dadas. Aplicando o método das cascas cilíndricas, calcule o volume do sólido obtido pela rotação da região em torno do eixo dado.
Passo 1
Se liga no gráfico dessas funções que estão no enunciado.
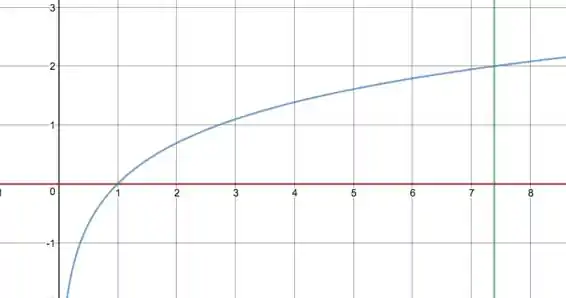
Lembrando que como temos que girar a função em torno do eixo , a integral que temos que calcular é:
Passo 2
Ora, se . Lembrando que esse . Quando vamos integrar com respeito a , a gente sempre pega a função que está mais a direita e subtrai daquela que está mais a esquerda. Então nossa integral ficou assim:
Agora, para encontrar os limites de integração, basta substituir os valores na função . Perceba que já temos um limite de integração:
Para
Passo 3
Vamos fazer cada uma dessas integrais separadamente:
Agora vamos para a próxima:
Nesse caso, vamos ter que fazer uma integração por partes. Lembra da fórmula?
Chamando e
Passo 4
Juntando tudo:
Resposta