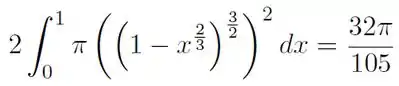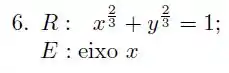
Passo 1
O lance é esboçar o mais precisamente possível os gráficos das funções pra entender bem a região :
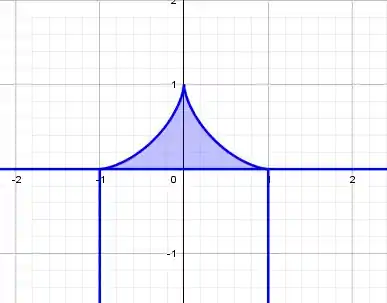
Passo 2
Então é a união de 2 pedaços de área idêntica, um que vai de a e outro que vai de a .
Daí pra facilitar nossa vida podemos montar uma só integral, que seria pra calcular o volume do sólido obtido pela rotação de um só desses pedaços, e multiplicar o resultado por 2.
Além disso, vamos reescrever aquela função implícita ali em cima da seguinte maneira:
Assim, o volume do sólido todo é:
Passo 3
Agora é só resolver a integral.
Resposta
Exercícios de Livros Relacionados
Determine o volume do sólido obtido com a rotação da região limitada por y = x e pelas retas y = 2 e x = 0 em torno Do eixo x .Do eixo y .Da reta y = 2 .Da reta x = 4 .
Volume de um toro. O disco x 2 + y 2 ≤ a 2 gira em torno da reta x = b ( ba ) para gerar um sólido em forma de rosquinha chamado toro. Determine seu volume. (Sugestão: ∫ - a a a 2 - y 2 d y = π a 2 /
42: A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x = y - 3 2 ,x = 4 ; em torno de y = 1 .
Por integração, determine o volume do sólido obtido pela rotação da região triangular com os vértices ( 0,0 ) , b , 0 e ( 0 , h ) em torno Do eixo x .Do eixo y .