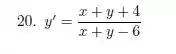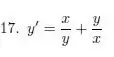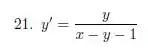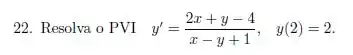Listas GMA de Cálculo IIA da UFF - Lista 9

Considere a equação da forma

Onde , , , , , são constantes reais.

1. Quando , pode-se reduzir essa equação em uma equação homogênea nas variáveis e se e , onde e são soluções do sistema linear.
2. Quando e e não simultaneamente nulos, pode-se reduzir essa equação em uma equação de variáveis separáveis nas variáveis e , se fizermos a substituiç��o
3. Quando e e não simultaneamente nulos, pode-se reduzir essa equação em uma equação de variáveis separáveis nas variáveis e , se fizermos a substituição

Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.

Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.

Nos exercícios 19 a 21 use o método desenvolvido na questão 18, para determinar a solução geral das equações.