Um cilindro rígido homogêneo de raio rola sem deslizar para a direita sobre o trecho AB de uma mesa horizontal com velocidade do centro de massa constante de módulo , como mostrado na figura, sendo o coeficiente de atrito estático entre o cilindro e o trecho AB da mesa.
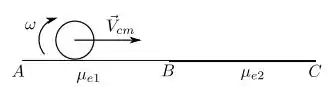
No avanço, entra no trecho BC, no qual o coeficiente de atrito estático com o cilindro é = .
Selecione a resposta correta:
- O momento angular do cilindro em torno de seu eixo de simetria permanece constante.
- O cilindro começa a deslizar.
- A velocidade de translação é duas vezes menor.
- O torque da força de atrito estática em relação ao eixo de simetria do cilindro é duas vezes maior.
- A energia cinética total diminui.
- O cilindro continua rolando sem deslizar, mas a condição de rolamento puro passa a ser .
Passo 1
Cara, o momento angular desse cilindro é igual a...
O momento de inércia não muda do cilindro não muda, agora... E a velocidade angular ? Será que ela muda?
Passo 2
NÃO! A velocidade angular só depende da rotação e a rotação não depende da força de atrito! A rotação depende apenas do torque feito no eixo do cilindro e a força de atrito não interfere nesse torque .
Portanto o momento angular continua o mesmo!
Resposta
Letra A