Três cilindros rígidos homogêneos idênticos rolam sem deslizar para a direita sobre uma mesa horizontal. Uma longa placa reta rígida está colocada encima deles e se desloca com velocidade constante módulo como mostrado na figura.
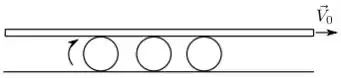
A placa não desliza sobre os cilindros e mantém contato com eles o tempo todo. Podemos afirmar que os cilindros avançam em conjunto com a mesma velocidade de translação de módulo
Passo 1
Cara... Os três rolos se movimentam tanto em relação ao chão quanto a placa sem deslizar. Isso significa que um ponto no chão tem a velocidade do chão (ou seja, ) e um ponto encostado na placa vai ter a mesma velocidade da placa:
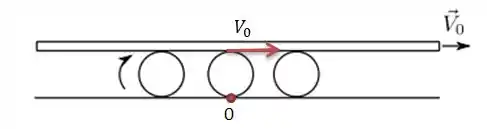
O que queremos saber é qual a velocidade de translação dos rolos, que é a velocidade do centro de massa de cada rolo:
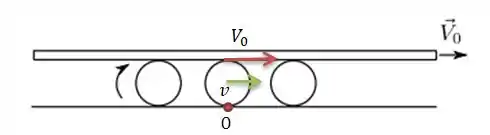
Vamos nessa?
Passo 2
Cara, se liga, cada ponto desse rolo vai ter dois tipos de velocidade que se somam.
A velocidade de translação e a velocidade de rotação.
A velocidade de translação (também conhecida como velocidade do centro de massa) é a velocidade que dá a direção para onde o rolo tá indo, que nesse caso é para a direita e ela é igual em todos os pontos do rolo.
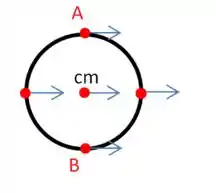
Já a velocidade proveniente do movimento de rotação, ela é dada pela expressão , portanto, para essa velocidade só existe a uma distância r do centro do rolo e essa velocidade aponta no sentido de rotação do rolo, no desenho abaixo ela está representada pelas setas vermelhas.
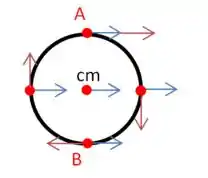
Passo 3
Como vimos no passo 1, o ponto B que é o ponto que está em contato com o solo tem velocidade zero, portanto a soma da velocidade de translação com a velocidade de rotação deve ser igual a zero.
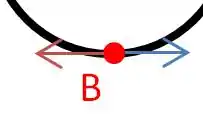
Para isso ocorrer, é necessário portanto que essas velocidades sejam iguais em módulo (isso sempre vai ocorrer na rotação sem deslizamento).
Já no ponto A, temos que a velocidade é igual a velocidade da placa que é .
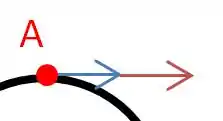
Nesse ponto, as velocidades se somam, e como sabemos que elas possuem o mesmo valor, podemos concluir portanto que a velocidade de translação é e que a velocidade de rotação na extremidade do rolo também é
Logo:
Passo 4
Agora é só partir para o abraço.Nessa questão, ele quer saber a velocidade no centro do rolo:
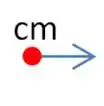
E nesse ponto só há velocidade de translação, pois a gente está olhando pro centro de massa desse rolo.
Sendo assim, a velocidade será
Passo 5
Resposta
Letra A.