Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Força de Atrito

Ver Teoria
Exercício 18123456789101112131415161719202122232425262728293031323334353637383940414243444546474849505152535455565758

Enunciado

Um bloco de massa m desliza para baixo num plano inclinado com velocidade constante desde uma altura h acima da base do plano inclinado até a base. O coeficiente de atrito cinético entre o bloco e o plano inclinado é μ . A energia dissipada pela força de atrito durante essa descida é

  1. m g h / μ
  2. m g h
  3. μ m g h / sin ⁡ θ
  4. m g h sin ⁡ θ
  5. 0

Passo 1

Primeiro vamos esquematizar isso, pode ser?

Temos aqui um plano inclinado de θ graus, altura h e um bloco nessa altura...

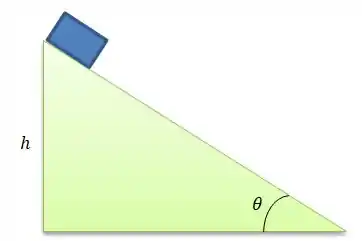
Esse bloco é solto com velocidade inicial 0 e começa a descer com velocidade constante (o que não aconteceria se o plano não tivesse atrito). A primeira pergunta a se fazer é: quais são as forças que atuam nesse bloco enquanto ele desce?

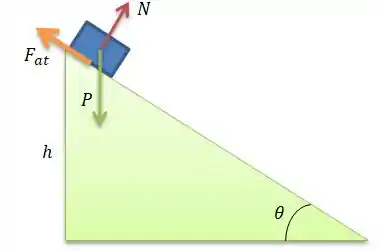
Veja se concorda: As forças que atuam nele é a força peso P , a normal N que chão faz no bloco, e a força de atrito F a t contrária ao movimento do plano.

POW! A única força que dissipa energia aí é a força de atrito F a t , e a energia dissipada por ela é igual ao trabalho que o bloco tem para descer até a base do plano (trabalho τ ).

E d i s s i p a d a = τ

Bora encontrar esse τ ?

Passo 2

Pow! Podemos encontrar trabalho de uma força multiplicando a força pela distância andada. No caso do bloco, ele anda do topo até a base. Essa distância vamos chamar de d ...

E d i s s i p a d a = F a t   d   →

Mas por trigonometria, podemos falar que essa distância d é igual a...

E d i s s i p a d a = F a t h sin ⁡ θ  

Agora vamos encontrar a força de atrito F a t , pode ser?

Passo 3

De acordo com a teoria, a força de atrito pode ser dada por...

F a t = μ N

Onde N é a orla desenhada no plano. Repare novamente no desenho que podemos encontrar a Normal novamente por trigonometria...

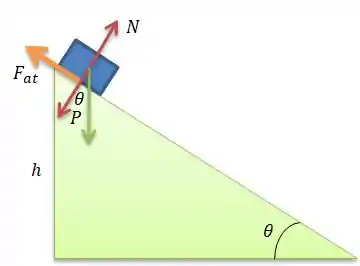
Então...

N = P cos ⁡ θ     →

N = m g cos ⁡ θ

Ou seja...

F a t = μ m g cos ⁡ θ

E portanto podemos concluir sobre a energia dissipada...

E d i s s i p a d a = F a t h sin ⁡ θ   →

E d i s s i p a d a = μ m g cos ⁡ θ h sin ⁡ θ   →

E d i s s i p a d a = μ m g cos ⁡ θ h sin ⁡ θ  

Mas pera! Tem algo estranho! Não temos essa resposta nos itens! Será que erramos alguma coisa?

Passo 4

Não! Não erramos não! Na verdade só está incompleta!

O problema disse que o bloco desce com velocidade constante. Isso significa que as forças na direção da rampa se cancelam! E quais são as forças na direção da rampa?

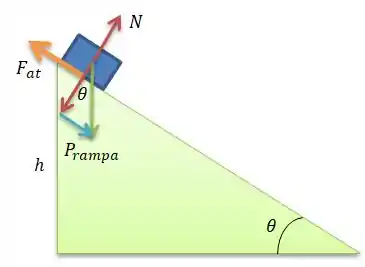
A força na direção da rampa é a componente P r a m p a (em azul) e a força de atrito F a t . Então, para o bloco descer em velocidade constante...

P r a m p a = F a t   →

Já vimos no passo anterior que a F a t = μ m g cos ⁡ θ . E por trigonometria podemos saber quem é a P r a m p a ...

m g sin ⁡ θ = μ m g cos ⁡ θ   →

1 = μ cos ⁡ θ sin ⁡ θ

Então...

E d i s s i p a d a = μ m g cos ⁡ θ h sin ⁡ θ     →

E d i s s i p a d a = m g h

Resposta

Letra B.

Exercícios de Livros Relacionados

12.17P A mesma esfera descrita no Problema 12.16 submerge em óleo SAE 30 à temperatura de 20 °C , cuja densidade é aproximadamente igual á da água. A) Calcule a velocidade terminal da esfera. B) Calcu
12.9E Uma pare-quedista com massa de 60kg salta com um paraquedas cuja área frontal é de 15m² ². Sabendo que a densidade do ar é ρ = 1,2kg.m³ ³ e que o coeficiente de arraste do paraquedas é C = 1,4 ,
Um operário arrasta um caixote no piso de uma fábrica puxando-o por uma corda. O operário exerce uma força de módulo F = 450N sobre a corda, que está inclinada de um ângulo θ = 38 ° em relação à horiz
Um caminhão transporta um caixote de 200k g a 90k m / h numa estrada horizontal. Avistando um obstáculo, o motorista fria, com desaceleração uniforme de 2,5m / s 2 , até parar. O caixote, em consequên
12.7E Uma placa de vidro molhada com área de 2,0m² ² é colocada sobre outra placa idêntica, e um filme de água com espessura de 3,0μm se forma entre elas. Uma força de cisalhamento de 50N é aplicada à