Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Colisões com Rotação

Ver Teoria
Exercício 261234567891011121314151617181920212223242527

Enunciado

Uma barra fina e homogênea de massa M e comprimento l está pendurada, verticalmente, por sua extremidade superior em um eixo horizontal em torno do qual pode girar sem atrito. Uma bala de massa m tem velocidade horizontal de módulo v 0 no plano em que a placa pode girar, atinge a barra em repouso a uma distância d de sua extremidade superior, e nela fica incrustada, conforme indica a figura.

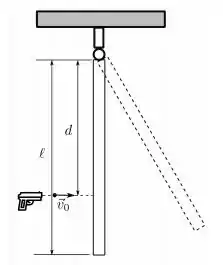
Nessas condições, o conjunto barra+bala adquire velocidade angular de módulo ω 1 logo após a colisão e então seu centro de massa eleva-se até uma altura máxima h . Sabendo que o momento de inércia da barra relativo ao eixo de rotação é 1 3 M l 2 , que d = l / 3 e M   =   11 m , podemos afirmar que

  1. ω 1 = v 0 / ( 4 3   l )           e               v 0 = 12 2 g h
  2. ω 1 = v 0 / ( 4 3   l )           e               v 0 = 12 3 g h
  3. ω 1 = 3 v 0 / ( 4   l )           e               v 0 = 12 2 g h
  4. ω 1 = 3 v 0 / ( 4   l )           e               v 0 = 12 3 g h
  5. ω 1 = v 0 / ( 4 3   l )           e               v 0 = 12 6 g h

Passo 1

Bem... Nesse problema vamos usar a conservação da quantidade de momento angular L , pois de acordo com as Leis da Física, podemos garantir que o momento angular do sistema (bala+bastão) não se altera, já que não há forças externas envolvidas no problema.

Então sendo assim, o momento angular inicial tem que ser igual ao momento angular final...

L i n i c i a l = L f i n a l

Bora lá?

Passo 2

O momento angular inicial, imediatamente antes da colisão, é dado apenas pelo momento da bala (já que ela é a única com movimento antes da colisão). O momento angular da bala quando ela está próxima ao bastão é...

L i n i c i a l = m v 0 d

Assim que a bala atinge o bastão ela o conjunto ganha uma velocidade angular ω 1 e possuem juntos um momento de inércia I t o t . De acordo com a teoria, nesse instante o momento angular L f i n a l .

L f i n a l = I t o t ω 1

O momento de inércia total vai ser igual ao momento de inércia da placa somado ao momento de inércia da bala de massa m que está presa a uma distância d do eixo de rotação...

L f i n a l = I p l a c a + m d 2 ω 1

Passo 3

Belezinha! Como o momento angular se conserva...

L i n i c i a l = L f i n a l

Cara, agora é só juntar essas duas coisa e ser feliz! Veja...

m v 0 d = I p l a c a + m d 2 ω 1   →

Pelo enunciado, sabemos quem é o momento de inércia da placa I p l a c a e sabemos também que d = l / 3 ...

m v 0 l 3 = 1 3 M l 2 + m l 2 3 ω 1   →

m v 0 l 3 = 1 3 M l 2 + m l 2 3 ω 1   →

m v 0 l 3 = l 2 3 M + m ω 1   →

Isolando ω 1 ...

3 m v 0 l 3 = M + m ω 1   →

ω 1 = 3 m v 0 l 3   M + m

Como M = 11 m ...

ω 1 = 3   m v 0 l 3 11 m + m   →

ω 1 = 3   m v 0 l 3   12 m   →

ω 1 = v 0 4 3   l    

Passo 4

Para a gente ver quem é a velocidade v 0 agora, precisamos trabalhar com o conceito de conservação de energia.

Sabemos que na hora que a bala atinge o bastão, o conjunto começa a girar com velocidade angular ω 1 . Isso faz com que o sistema tenha energia cinética rotacional...

K = 1 2 I t o t ω 1 2       →

O I t o t a gente já calculou e o ω 1 também. Então é só aplicação!

K = 1 2 ⋅ l 2 3 M + m v 0 4 3   l   2   →

K = 1 2 ⋅ l 2 3 12 m v 0 4 3   l   2     →

K = 2 m l 2 ⋅ v 0 2 16 ⋅ 3   l 2     →

K = m ⋅ v 0 2 8 ⋅ 3    

Só que o problema nos disse que essa energia se transforma em energia potencial, já que o conjunto ( M + m ) ganha uma altura h ...

E p o t e n c i a l = M + m g h

Então, como a energia cinética antes deve ser a energia a ser armazenada nessa energia potencial, temos que K = E p o t e n c i a l . Então...

m ⋅ v 0 2 8 ⋅ 3     = 12 m g h   →

v 0 2 8 ⋅ 3     = 12 g h   →

v 0 2 = 12 ⋅ 24 g h   →

v 0 = 12 2 g h  

Resposta

Letra A.

Exercícios de Livros Relacionados

Um parquinho possui um pequeno carrossel com 1,20m de raio e uma massa de 180k g . O raio de giração do carrossel (veja o problema 79 do Capítulo 10) é 91,0c m . Uma criança com 44,0k g de massa corre
Uma barra fina e homogênea com 0,5 m de comprimento e 4 k g de massa pode girar em um plano horizontal em torno de um eixo vertical que passa pelo centro da barra. A barra está em repouso quando uma b
Se, no sistema do Problema 64, L = 1,2m , M = 0,80k g , m = 0,30k g , e o maior ângulo entre a barra e a vertical após a colisão é 60 ° , determine a rapidez da partícula antes do impacto.
Um haltere formado por dois discos 1 e 2 iguais, de massa m , unidos por uma barra rígida de massa desprezível e comprimento l = 30c m , repousa sobre uma mesa de ar horizontal. Um terceiro disco 3 de
Uma esfera maciça com 36,0N de peso sobe rolando um plano inclinado com um ângulo de 30,0 ° . Na base do plano inclinado, o centro de massa da esfera possui uma velocidade de translação de 4,90m / s .