Um disco horizontal gira com velocidade angular em torno do eixo vertical que passa pelo seu centro. Uma moeda de massa é posta sobre o disco a uma distância do eixo de rotação.
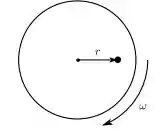
Qual deve ser o coeficiente de atrito mínimo entre a moeda e o disco para que não haja deslizamento?
Passo 1
POW! Antes de tudo, vamos desenhar aqui o diagrama de corpos livres para a gente descobrir quais forças estão agindo sobre a moeda:
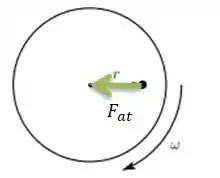
Repare que assim que você coloca a moeda em cima do disco, ela começa a girar com o disco. Para impedir que o disco jogue a moeda para longe, precisamos garantir que exista atrito entre a moeda e o disco e que esse atrito atua justamente como a força centrípeta !
Mas veja bem, a força que existe é a força de atrito e ela atua como uma força centrípeta, ta ligado?
Ta, mas e daí?
Bem, queremos o coeficiente de atrito mínimo para a moeda não ser arremessada. E sabemos pela teoria que toda força de atrito pode ser escrita como...
Onde é a força normal e o coeficiente de atrito que queremos encontrar. Vamos nessa?
Passo 2
Como não existe movimento na pra baixo ou pra cima na moeda, podemos dizer que a normal é igual ao peso da moeda...
Então...
Só que como vimos no passo anterior, à força de atrito na moeda atua como força centrípeta, colocando a moeda em um movimento giratório. Força centrípeta pode ser dada por...
Então...
Como em um movimento circulatório sem escorregamento podemos dizer que a relação entre a velocidade tangencial e a velocidade angular é dada por...
Então...
Resposta
Letra A