Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Cálculo do Momento de Inércia de Partículas

Ver Teoria
Exercício 131234567891011121415161718192021222324252627282930313233343536373839

Enunciado

Um sistema é constituído de quatro massas iguais ligadas por arames rígidos de massas desprezíveis formando um quadrado plano de lado a, no qual as massas estão localizadas nos vértices.

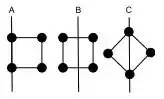
São calculados os momentos de inércia I A , I B e   I C relativos aos respectivos eixos A, B e C, mostrados na figura. O eixo A passa lateralmente pelas duas massas, o eixo B pelo centro do quadrado a a / 2 de dois lados e o eixo C na diagonal. Podemos afirmar, para os momentos de inércia I A , I B e   I C , que

  1. I A > I B = I C
  2. I A = I B = I C
  3. I A = I C > I B
  4. I A = I C < I B
  5. I A < I B < I C
  6. I A > I B > I C

Passo 1

Bem... Temos aqui um problema de comparar momentos de inércias. Sabemos pela teoria que o momento de inércia de um sistema de partículas de N massas m em relação a um eixo qualquer pode ser dado por...

I = ∑ i = 1 N m i d i 2

Onde d i é a distância da i - é s i m a partícula ao eixo em que estamos calculando o momento de inércia.

Também pode adiantar o nosso trabalho aqui nesse problema, observar que o eixo de A é paralelo ao eixo de B (eixo que passa pelo centro de massa do quadrado)...

Sendo assim, vamos também poder aplicar o teorema dos eixos paralelos! Vamos nessa?

Passo 2

Podemos aplicar o Teorema dos eixos paralelos sempre que tivermos um eixo paralelo a um eixo que passa pelo centro de massa. Veja que o eixo de B passa pelo centro de massa e o eixo de A é paralelo ao eixo de B

Pelo teorema dos eixos paralelos então...

I A = I B + M l 2

Onde M é a massa total das 4 partículas e l é a distância do eixo A ao eixo que passa pelo centro no caso é l = a / 2 . Então veja que só por essa equação dos eixos paralelos já podemos dizer que...

I A > I B

Passo 3

Agora vamos analisar a relação de I C com I B . Partiu?

Para isso, vamos usar a fórmula de momento de inércia...

I = ∑ i = 1 N m i d i 2

E calcular o momento para I C ...

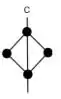
Veja que temos duas massas que passa pelo eixo, logo a distância d i delas em relação ao eixo é 0 , enquanto isso temos outras duas massas cuja distância delas ao eixo é a 2 / 2 pela trigonometria, saca?

I C = m 0 + m 0 + m   a 2 / 2 2 + m   a 2 / 2 2   →

I C = 2 m   a 2 2 2 →

I C = 2 m   2 a 2 4 →

I C = m   a 2

Agora calculemos o momento de inércia de I B ...

Veja que nesse caso, todas as massas estão a uma distância de a / 2 do eixo...

I B = m   a 2 2 + m   a 2 2 + m   a 2 2 + m   a 2 2

I B = m a 2 4 + m a 2 4 + m a 2 4 + m a 2 4

Então...

I B = 4 m a 2 4   →

I B = m a 2

Ou seja...

I B = I C

Então...

I A > I B = I C

Resposta

Letra A.

Exercícios de Livros Relacionados

1. O centro de massa do haltere da FIGURA Q12.1 encontra-se no ponto a, b ou c? Explique.
Uma viga de 40k g e 5,0m de comprimento é sustentada, sem estar fixada, pelas duas pilastras mostradas na FIGURA P12.64. Um garoto de 20k g começa a caminhar ao longo da viga. Quão próximo ele pode ch
Integrando diretamente, calcule o momento de inércia de uma haste delgada de Massa M e comprimento L em torno de um eixo localizado a uma distância d de uma das extremidades. Confirme se sua resposta
Uma viga rígida com 3,0m de comprimento e massa de 100k g é apoiada em cada extremidade. Um estudante de 80k g encontra-se em pé a 2,0m do suporte 1. Que valor de força cada suporte exerce sobre a vig
Para o sistema de quatro partículas da figura 9-45, (a) determine o momento de inércia I x em relação ao eixo x que passa por m 2 e m 3 e (b) determine o momento de inércia I y em relação ao eixo y qu