Uma pequena bola de massa está presa em um fio, apoiada em uma mesa horizontal e sem atrito. A bola executa um movimento circular uniforme com velocidade angular inicial e raio . O fio passa por um furo na mesa. Uma pessoa então puxa o fio lentamente até que o raio da trajetória final torne-se .
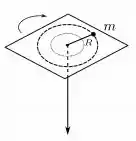
Seja o módulo do momento angular inicial da bola e o módulo do seu momento angular final. Do mesmo modo, é a energia cinética inicial e a energia cinética final. Podemos dizer que
Passo 1
POW! Estamos lidando aqui com uma questão de conservação da quantidade de momento angular.
Cara... Anota aí: o momento angular sempre se conserva se não houver torque externo no sistema. A energia cinética não necessariamente.
A bolinha estava girando...
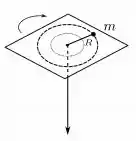
E de repente surge uma força que puxa essa bolinha para o centro. Então vem a pergunta. Será que houve torque nessa parada?
Passo 2
Bem... Podemos afirmar que houve sim forças externas, pois o sistema é constituído só pela bolinha e de repente alguém (de fora) puxa a bolinha em direção ao centro. Só que olha que maneiro... Essa força externa foi uma força radial aumentando apenas a força centrípeta...
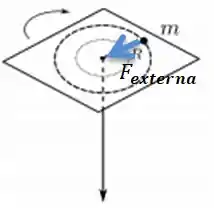
POW! Mas essa força não gera nenhum torque na bolinha! Afinal, ela uma força paralela ao raio de rotação, ta ligado?
Bem... Se não há torque externo (embora haja força externa), então podemos garantir que o momento angular do sistema se conserva, ou seja...
Passo 3
Quanto à energia cinética do sistema, como temos uma bolinha girando, a energia cinética que ela vai ter vai ser a energia cinética rotacional...
Mas poxa! Momento angular é definido como , portanto...
E para a energia cinética final...
Só que sabemos se o momento angular temos que apenas ver o que acontece com a velocidade angular! Se a velocidade angular final for maior que a inicial , então a energia cinética final vai ser maior que a inicial, saca?
Passo 4
Pow! Então como que a gente pode “quantificar” essa velocidade angular?
Bem... Sabemos que o momento angular é definido por ...
O momento de inércia por sua vez é definido por ...
Mas o raio final da trajetória é a metade do raio inicial...
Beleza! Então a velocidade angular final é maior que a inicial! Isso significa que a energia cinética final também será maior que a energia cinética inicial...
Resposta
Letra B.