Dois discos homogêneos A e B de massas e raios iguais são fixados por pinos em uma parede vertical, em torno dos quais podem girar sem atrito. Enrola-se em cada um deles um fio ideal em sua periferia, sobre a qual o fio não desliza, e penduram-se blocos de massa iguais a , como mostra a figura.
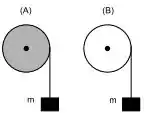
Ao serem os discos A e B libertados a partir do repouso, medem-se, respectivamente, suas acelerações angulares e e os torques sobre eles e , calculados em relação ao centro dos discos. Pode-se relacioná-los corretamente como na opção:
Passo 1
POW! Nesse problema vamos utilizar os conceitos de cinemática rotacional, e para resolvê-lo eu quero que você tenha em mente duas coisas:
- O torque depende apenas da força aplicada e da distância dessa força ao centro de rotação.
- A aceleração angular , sabendo o torque, pode ser calculada pela equação...
Então bora analisar esses dois itens!
Passo 2
Como já comentei ali no passo anterior, o torque depende apenas da força aplicada e da distância dessa força ao eixo de rotação. Observe que no nosso caso, a força aplicada é a mesma nos dois casos (é a força peso do bloquinho )...
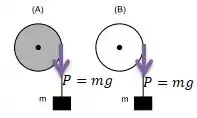
E a distância de aplicação das forças em relação ao eixo de rotação também será a mesma (distância )...
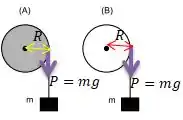
Sendo assim, podemos afirmar que os torque de e são os mesmos!
Passo 3
Por outro lado, sabemos ser a massa de maior que a massa de ...
Isso faz com que os momentos de inércias sigam a mesma lógica...
Então, agora podemos comparar as acelerações angulares...
Como e , podemos afirmar que...
Resposta
Letra D