Uma correia ideal liga dois discos homogêneos de raios idênticos a e massas e , cuja distância entre os seus centros é . Os seus centros estão fixos por pinos em torno dos quais cada disco pode girar sem atrito. Uma correia tensa e inextensível passa pelas periferias dos discos, sem deslizar sobre elas, e move-se com velocidade de módulo constante , como indica a figura.
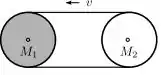
Sabendo-se que o momento de inércia de um disco homogêneo de massa e raio para um eixo que passa pelo seu centro e perpendicular a sua superfície é , podemos afirmar para o módulo do momento angular total do sistema constituído pelos discos, relativo ao seu centro de massa, que
Passo 1
POW! De acordo com a nossa Teoria, o momento angular de um disco em rotação sempre pode ser dado por...
O momento angular então de dois discos em rotação com a mesma velocidade será...
Repare que usamos a mesma velocidade angular nas duas, pois os dois discos possuem o mesmo raio e a mesma velocidade tangencial , então certamente a velocidade angular dos dois será a mesma!
Sendo assim, o módulo do momento angular total do sistema em relação ao seu centro de massa será...
Passo 2
Bem, de acordo com a teoria, o momento de inércia do disco é dado por ...
O enunciado também nos disse que as massas de cada disco valem para o disco e para o segundo disco...
Como pela teoria ...
Resposta
Letra A.