Listas de Estudos pra Prova - Halliday Vol 1 - 8°ed de Física 1 da UTFPR - Movimento Retilíneo

(Cap 2 – Ex 19) Em um certo instante de tempo, uma partícula tinha uma velocidadede no sentido positivo de ; depois, a velocidade era no sentido oposto. Qual foi a aceleração média da partícula durante este intervalo de 2,4 s?

(Cap 2 – Ex 3) Durante um espirro, os olhos podem se fechar por até . Se vocês está dirigindo um carro a e espirra, de quanto o carro pode se deslocar até vocês abrir novamente os olhos?

(Cap 2 – Ex 2) Um carro sobe uma ladeira com uma velocidade constante de e desce a ladeira com uma velocidade constante de . Calcule a velocidade escalar média da viagem ida e volta.

(Cap 2 – Ex 8) Para estabelecer um recorde de velocidade em uma distância (em linha reta), um carro deve percorrer a distância primeiro em um sentido (em um tempo ) e depois no sentido oposto (em um tempo ). (a) Para eliminar o efeito do vento e obter a velocidade do carro na ausência de vento, devemos calcular a média aritmética de e (método 1) ou devemos dividir pela média aritmética de e ? (b) Qual é a diferença percentual dos dois métodos se existe um vento constante na pista e a razão entre a velocidade do vento e a velocidade do carro é ?

(Cap 2 – Ex 4) Calcule a velocidade média nos dois casos seguintes:

(a) você caminha a uma velocidade de e depois corre a em uma pista reta;

(b) você caminha com uma velocidade de e depois corre por a em uma pista reta.

(c) Faça o gráfico de x em função de t nos dois casos e indique de que forma a velocidade média pode ser determinada a partir do gráfico.

(Cap 2 – Ex 1) Um automóvel viaja em uma estrada retilínea por a .Em seguida, continuando no mesmo sentido, percorre outros a .

(a) Qual é a velocidade média do carro durante este percurso de ?(Suponha que o carro está se movendo no sentido positivo de ).

(b) Qual é a velocidade escalar média?

(c) Desenhe o gráfico de em função de e mostre como calcular a velocidade média a partir do gráfico.

(Cap 2 – Ex 25) Suponha que uma nave espacial se move com uma aceleração constante de , o que dá aos tripulantes a ilusão de uma gravidade normal durante o voo.

(a) Se a nave parte do repouso, quanto tempo leva para atingir um décimo da velocidade da luz, que é 3,0 × m/s?

(b) Que distância a nave percorre nesse tempo?

(Cap 2 – Ex 20) A posição de uma partícula que se move ao longo do eixo x é dada por , onde está em metros e em segundos. Determine (a) a posição, (b) a velocidade e (c) a aceleração da partícula em . (d) Qual é a coordenada positiva máxima alcançada pela partícula e (e) em que instante de tempo é alcançada? (f) Qual é a velocidade positiva máxima alcançada pela partícula e (g) em que instante de tempo é alcançada? (h) Qual é a aceleração da partícula no instante em que a partícula não está se movendo (além do instante )? (i) Determine a velocidade média da partícula entre e .

(Cap 2 – Ex 9) Você tem que dirigir em uma via expressa para se candidatar a um emprego em outra cidade, que fica a de distância. A entrevista foi marcada para as e Você planeja dirigir a e parte às para ter algum tempo de sobra. Você dirige na velocidade planejada durante os primeiros , mas, em seguida, um trecho em obras o obriga a reduzir a velocidade para por . Qual é a menor velocidade que deve manter no resto da viagem para chegar a tempo?

(Cap 2 – Ex 13) Você dirige do Rio a São Paulo metade do tempo a e a outra metade a . Na volta, você viaja metade da distância a e a outra metade a . Qual é a velocidade escalar média (a) na viagem do Rio a São Paulo, (b) na viagem de São Paulo ao Rio, e (c) na viagem inteira? (d) Qual é a velocidade média na viagem inteira? (e) Plote o gráfico de em função de para o item (a), supondo que o movimento ocorre no sentido positivo de

. Mostre de que forma a velocidade média pode ser determinada a partir do gráfico.

(Cap 2 – Ex 14) A função posição de uma partícula que está se movendo ao longo do eixo é , com em metros e em segundos. (a) Em que instante e (b) em que posição a partícula para (momentaneamente)? Em que (c) instante negativo e (d) instante positivo a partícula passa pela origem? (e) Plote o gráfico de em função de para o intervalo de a . (f) Para deslocar a curva para a direita no gráfico, devemos acrescentar a o termo ou o termo ? (g) Essa modificação aumenta ou diminui o valor de para o qual a partícula para momentaneamente?

(Cap 2 – Ex 21) A posição de uma partícula que se desloca ao longo do eixo varia com o tempo de acordo com a equação , onde está em metros e em segundos. Quais são as unidades (a) da constante e (b) da constante ? Suponha que os valores numéricos de e são e , respectivamente. (c) Em que instante a partícula passa pelo maior valor positivo de ? De a , (d) qual é a distância percorrida pela partícula e (e) qual é o deslocamento? Determine a velocidade da partícula nos instantes (f) , (g) , (h) e (i) . Determine a aceleração da partícula nos instantes U) , (k), (1) e (m) .

(Capítulo 2.7 – Exercício 43) Você está discutindo no telefone celular enquanto segue um carro de polícia não identificado, a de distância; os dois veículos estão a . A discussão distrai sua atenção do carro de polícia por (tempo suficiente para você olhar para o telefone e exclamar: "Eu me recuso a fazer isso!"). No início desses , o policial freia bruscamente, com uma desaceleração de .

(a) Qual é a distância entre os dois carros quando você volta a prestar atenção no trânsito?

Suponha que você leve outros para perceber o perigo e começar a frear

(b) Se você também freia com uma desaceleração de , qual é a velocidade do seu carro quando você bate no carro de polícia?

(Capítulo 2 – Problemas Adicionais – Exercício 106) Deixa-se cair uma pedra, sem velocidade inicial, do alto de um edifício de . A que distância do solo está a pedra antes de chegar ao solo?

(Capítulo 2.9 – Exercício 45) Em um prédio em construção, uma chave de grifo chega ao solo com uma velocidade de . (a) De que altura um operário a deixou cair? (b) Quanto tempo durou a queda? (c) Esboce os gráficos de , e em função de para a chave de grifo.

(Capítulo 2.10 – Exercício 67) Que distância percorre em um corredor cujo gráfico velocidade-tempo é mostrado na Fig. 2-30? A escala vertical do gráfico é definida por

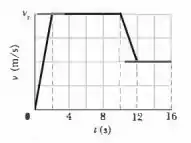
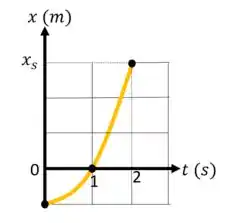
(Capítulo 2.7 – Exercício 35) A Fig. mostra o movimento de uma partícula que se move ao longo do eixo x com aceleração constante. A escala vertical do gráfico é definida por. Quais são (a) o módulo e (b) o sentido da aceleração da partícula?

(Capítulo 2.9 – Exercício 49) Um balão de ar quente está subindo a uma taxa de e está a acima do solo quando um tripulante deixa cair um pacote.

Quanto tempo o pacote leva para atingir o solo?

Com que velocidade atinge o solo?

(Capítulo 2.9 – Exercício 56) Uma pedra é deixada cair em um rio a partir de uma ponte situada acima da água. Outra pedra é atirada verticalmente para baixo após a primeira ter sido deixada cair. As pedras atingem a água ao mesmo tempo.

Qual era a velocidade inicial da segunda pedra?

Plote a velocidade em função do tempo para as duas pedras, supondo que é o instante em que a primeira pedra foi deixada cair

(Capítulo 2.7 – Exercício 26) Em uma estrada seca, um carro com pneus novos é capaz de frear com uma desaceleração constante de . (a) Quanto tempo esse carro, inicialmente se movendo a , leva para parar? (b) Que distância o carro percorre nesse tempo? (c) Desenhe os gráficos de em função de e em função de durante a desaceleração.

(Capítulo 2.7 – Exercício 30) Os freios de um carro podem produzir uma desaceleração da ordem de . (a) Se o motorista está a e avista um policial rodoviário, qual é o tempo mínimo necessário para que o carro atinja a velocidade máxima permitida de ? (A resposta revela a inutilidade de frear para tentar impedir que a alta velocidade seja detectada por um radar ou por uma pistola de laser.) (b) Desenhe os gráficos de em função de e em função de durante a desaceleração.