Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 2 – seção 6 – Problema 21.
(Cap 2 – Ex 21) A posição de uma partícula que se desloca ao longo do eixo varia com o tempo de acordo com a equação , onde está em metros e em segundos. Quais são as unidades (a) da constante e (b) da constante ? Suponha que os valores numéricos de e são e , respectivamente. (c) Em que instante a partícula passa pelo maior valor positivo de ? De a , (d) qual é a distância percorrida pela partícula e (e) qual é o deslocamento? Determine a velocidade da partícula nos instantes (f) , (g) , (h) e (i) . Determine a aceleração da partícula nos instantes U) , (k), (1) e (m) .
Passo 1
Falaiii meus amores, show de bolinhas?
Bora lá?
Pessoal, vamos ter que fazer um estudo da unidade. Basicamente é o seguinte: Se está em metros, o que está do outro lado do sinal de igual também deve estar em metro, ok?
Cada parcela deve estar em metros, então vamos igualar cada uma dessas parcelas a unidade metros.
Passo 2
atinge seu maior valor quando , vamor derivar para encontrar e igualar a zero.
Agora vamos substituir esses valores de na função posição:
Logo, a é no instante que a partícula passa por seu maior valor de .
Passo 3
Para descobrir a distância percorrida vamos usar integral. A distância percorrida será igual a área entre e o eixo dentrodo intervalo de tempo desejado.
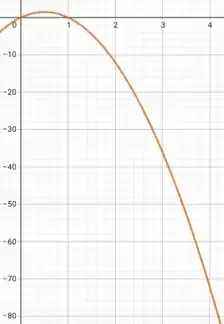
Entre e , a velocidade é positiva e, por isso, o deslocamento entre o gráfico de e o eixo vai ser igual a integral de nesse intervalo.
Entre e , a velocidade é negativa e, por isso, o deslocamento vai ser MENOS o valor da integral de nesse intervalo.
Então a partícula percorre uma distância:
Passo 4
O deslocamento é o entre e .
Passo 5
Para descobrir a velocidade em cada instante de tempo é só substituir o valor de em .
Passo 6
A aceleração é a derivada da velocidade, então se .
Resposta
a)
b)
c)
d)
e)
f)
g)
h)
i)
j)
k)
l)
m)