Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 2 – seção 4 – Problema 3.
(Cap 2 – Ex 3) Durante um espirro, os olhos podem se fechar por até . Se vocês está dirigindo um carro a e espirra, de quanto o carro pode se deslocar até vocês abrir novamente os olhos?
Passo 1
Falaiii galerinha do Responde ai, show de bola?
Bora resolver essa juntinho comigo?
Simboráaa
Bom pessoal, essa questãonão é tão difícil . Basta calcularmos quanto o carro se desloca durante , sabendo que ele está a uma velocidade de .
!!Cuidado: Com as unidades de mediada. Não podemos utilizar velocidade em e tempo em segundos. Temos que equivaler as unidades (ou passa para ou passa para hora).
Observação importante: Taxa de conversão de para (e vice-versa):
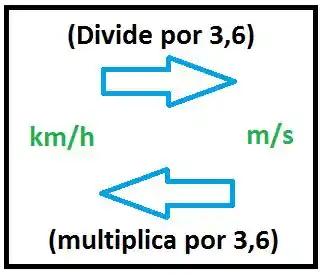
E, o que queremos calcular? Deslocamento de um carro que está a durante o tempo de uma espirro ().
Passo 2
Primeiramente, vamos transformar para :
Agora, utilizaremos a fórmula de velocidade média e isolaremos o para descobrir o deslocamento do carro:
logo,
Resposta
O carro pode se deslocar até metros durante o espirro (considerando velocidade do carro de e tempo do olho fechado no espirro de segundos).
Beleza pessoal ? Continuem fazendo exercícios com a gente , adoramos ter vocês por aqui!!!