Halliday - Vol.1 - Ed. 8 - Capítulo 2 – Seção 7 – Questão 26
(Capítulo 2.7 – Exercício 26) Em uma estrada seca, um carro com pneus novos é capaz de frear com uma desaceleração constante de . (a) Quanto tempo esse carro, inicialmente se movendo a , leva para parar? (b) Que distância o carro percorre nesse tempo? (c) Desenhe os gráficos de em função de e em função de durante a desaceleração.
Passo 1
Olááá meu amigo físico! Vamos matar esse probleminha de movimento retilíneo
Vamos assumir que é a estrada da sua cidade que ele ta falando, e aí nessa estrada, o carro freia com desaceleração constante de
Aí o exercício ta pedindo algumas informações a partir disso ok? Pra encontrarmos esses dados, é importante lembrarmos de algumas fórmulas, como o vovô ama titia:
E também a equação de Torricelli:
Então bora?
Passo 2
(a) Pessoal, vamos usar a função horária da velocidade para achar o tempo que o carro leva para parar.
Para achar o tempo, vamos isolar ele na equação, tal que:
Queremos o tempo que ele leva até para, ou seja, a velocidade final deve ser nula, . Enquanto isso, a velocidade inicial é de .
Substituindo as informações que temos, vamos descobrir que:
Então:
Logo, o carro demora segundos pra freiar nessa estrada 😉
Passo 3
(b) Podemos encontrar a distância percorrida em pela equação de Torricelli:
Isolando :
Substituindo os valores:
Então, até freiar, o carro percorreu . Pouquinho pra um carro né? Ta de boa!
Passo 4
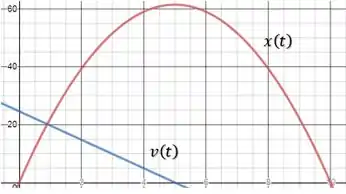
(c) Agora vamos plotar os gráficos!
A função horária da velocidade é:
Substituindo os valores encontramos que:
A função horária da posição é:
Substituindo os valores:
Então se a gente plotar o gráfico dessas duas funções, então:
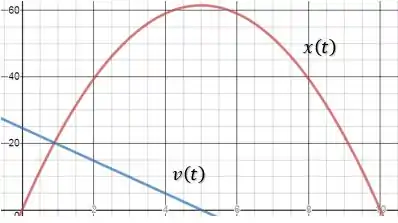
O gráfico vermelho é e o azul .
E finalizamosss
Resposta
a)
b)
(c) 