Halliday - Vol.1 - Ed. 8 - Capítulo 2 – Seção 9 – Questão 56
(Capítulo 2.9 – Exercício 56) Uma pedra é deixada cair em um rio a partir de uma ponte situada acima da água. Outra pedra é atirada verticalmente para baixo após a primeira ter sido deixada cair. As pedras atingem a água ao mesmo tempo.
Qual era a velocidade inicial da segunda pedra?
Plote a velocidade em função do tempo para as duas pedras, supondo que é o instante em que a primeira pedra foi deixada cair
Passo 1
Oiii gente, vamos lá pra mais um probleminha
Vamos fazer um diagrama do momento em que a segunda pedra é atirada ao rio, após a primeira ter caído.
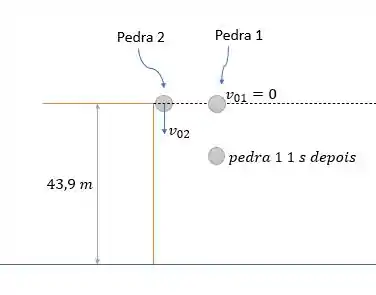
Sabendo que a velocidade inicial da pedra é nula, a equação da posição da pedra será de:
A partir dessa equação, podemos encontrar , o tempo que a primeira pedra demora pra cair
E aí, sabendo que a segunda pedra cai 1 segundo depois, podemos encontrar a partir de
Vamos lá!
Passo 2
a) Temos
Onde a aceleração da gravidade é a aceleração de queda das duas pedras e considerando como o tempo de queda dessa pedra nós temos:
Então a pedra leva 2.99 segundos para cair.
Passo 3
Agora vamos escrever a equação de movimento da pedra .
Considerando o tempo de queda dessa pedra e sabendo que as duas pedras caem tocam o chão ao mesmo tempo com a pedra 2 tendo partido depois da pedra 1. Com essas informações, o tempo de queda da pedra será de:
Logo, quando a pedra toca o chão nós teremos uma velocidade inicial de:
Passo 4
b) Agora vamos pros gráficos
Reescrevendo a equação de posição da pedra 1 nós temos:
Derivando isso no tempo, temos a velocidade da pedra 1:
Já a equação da posição da pedra será:
Considerando já que pelo enunciado da letra é o instante em que a primeira pedra (pedra 1) foi deixada cair. Derivando isso no tempo nós temos a equação da velocidade da pedra 2 como:
Plotando os dois gráficos nós temos:
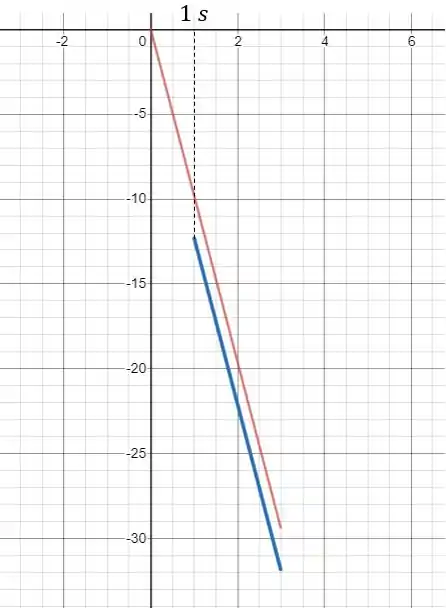
Com a reta vermelha sendo a pedra 1 e a reta azul a segunda note que a reta azul começa em 1s e termina no mesmo tempo que cessa a reta vermelha.
E é issoooo