Halliday - Vol.1 - Ed. 8 - Capítulo 2 – Seção 9 – Questão 45
(Capítulo 2.9 – Exercício 45) Em um prédio em construção, uma chave de grifo chega ao solo com uma velocidade de . (a) De que altura um operário a deixou cair? (b) Quanto tempo durou a queda? (c) Esboce os gráficos de , e em função de para a chave de grifo.
Passo 1
Olááá galera, que sacanagem a chave cair lá do alto né hahahaah
Mas nossa função aqui como super físicos é encontrar de que altura essa chave caiu e quanto tempo durou a queda
Para isso, vamos lembrar da equação de Torricelli:
Do vovô ama titia:
E do sorvetão:
Boraaa
Passo 2
a) Pessoal, vamos usar a equação de Torricelli para descobrir a altura, sabendo que a velocidade inicial é zero.
Isolando :
Como , então:
Passo 3
b) Podemos encontrar o tempo pela equação horária da velocidade.
Isolando :
Então a chave demora esse tempo pra cair:
Passo 4
c) Agora vamos plotar os gráficos
Pela função horária da posição, temos:
A velocidade é a derivada da posição e a aceleração é a derivada da velocidade, então temos:
No gráfico, está em vermelho, em azul e em verde.
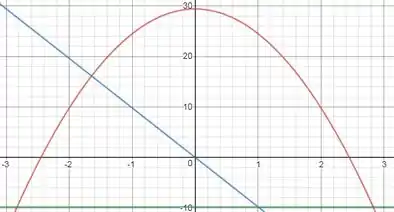
Showww!
Resposta
a)
b)