Halliday - Vol.1 - Ed. 8 - Capítulo 2 – Seção 7 – Questão 30
(Capítulo 2.7 – Exercício 30) Os freios de um carro podem produzir uma desaceleração da ordem de . (a) Se o motorista está a e avista um policial rodoviário, qual é o tempo mínimo necessário para que o carro atinja a velocidade máxima permitida de ? (A resposta revela a inutilidade de frear para tentar impedir que a alta velocidade seja detectada por um radar ou por uma pistola de laser.) (b) Desenhe os gráficos de em função de e em função de durante a desaceleração.
Passo 1
Oieee! Parece que alguém está querendo evitar uma multa, não é? Hahahaha
O primeiro passo de todos nessa questão é passar as velocidades de para , para isso é só dividir elas por .
E aí baseado na pessoinha que quer evitar os pontos na carteira, o exercício pede algumas informações pra gente, e pra encontrarmos essas informações vamos lembrar de algumas fórmulas, como o vovô ama titia:
E também a equação horária da posição:
Então vamos lá!
Passo 2
a) Os freios têm que produzir uma desaceleração constante igual para que o tempo seja mínimo. Vamos descobrir esse tempo? Então vamos precisar da função horária da velocidade!
Isolando o :
Agora é só substituir os valores em :
Então, o motorista teria que frear antes para não ser multado hehehe
Passo 3
b) Agora vamos de gráficos
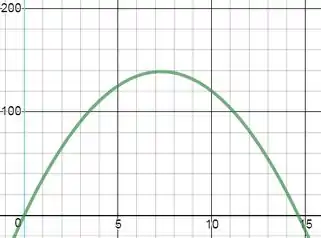
A função horária da posição é
Substituindo os valores, encontramos:
No gráfico, o eixo horizontal está em segundos e o eixo vertical em metros.
Passo 4
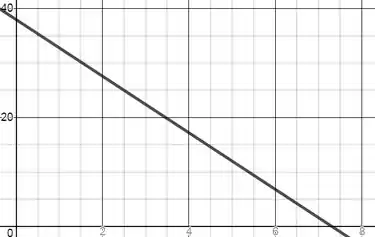
A função horária da velocidade é
Substituindo os valores conhecidos, encontramos:
No gráfico o eixo horizontal está em segundos e o vertical em m/s:
E é isso aí!
Resposta
a) 2,5 segundos
b) Velocidade: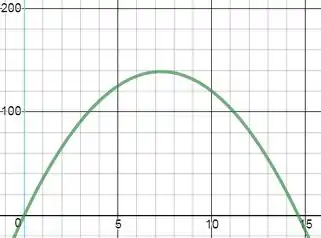 
Espaço: 