Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Deslocamento X Distância Percorrida

Ver Teoria
Exercício 2812345678910111213141516171819202122232425262729303132333435363738

Enunciado

Fundamentos de Fisica - Vol. 1. Halliday - 8ª Edição, Capítulo 2 – seção 4 – Problema 13.

(Cap 2 – Ex 13) Você dirige do Rio a São Paulo metade do tempo a 55   k m / h e a outra metade a 90   k m / h . Na volta, você viaja metade da distância a 55   k m / h e a outra metade a 90   k m / h . Qual é a velocidade escalar média (a) na viagem do Rio a São Paulo, (b) na viagem de São Paulo ao Rio, e (c) na viagem inteira? (d) Qual é a velocidade média na viagem inteira? (e) Plote o gráfico de x em função de   t para o item (a), supondo que o movimento ocorre no sentido positivo de

x . Mostre de que forma a velocidade média pode ser determinada a partir do gráfico.

Passo 1

É isso aí galerinhaa !! Animados ??

Esperso que super, ein !!

Antes de começar, a letra (a) nos pede a velocidade média ao longo do trajeto Rio – São Paulo, então vamos fazer um desenho esquematizando a situação descrita:

Vamos lembrar como calcular a velocidade média?

v m é d i a = d t

Então precisamos achar a distância, não é?

A distância é dada por:

d = v t

Então a distância total será:

d = 55 k m h t 2 + 90 k m h t 2

d = 72,5 k m h t

Substituindio na fórmula da velocidade média:

v m é d i a = 72,5 k m h t t

= 72,5 k m h

Podemos aproximar:

v m é d i a ≈ 73 k m h

Passo 2

Na viagem de volta nós temos algo parecido:

Aqui nós já temos a distância percorrida em cada trecho, então precisamos achar o tempo:

t = d v

Então o tempo total:

t = d 2 55 k m h + d 2 90 k m h = d 110 k m h + d 180 k m h

= 180 k m h d + 110 k m h d 19800 k m 2 h 2

t = 290 d 19800 k m h

Aplicando na fórmula da velocidade média:

v m é d i a = d t = d 290 d 19800 k m h

= 19800 k m h 290

= 68,3 k m h

v m é d i a ≈ 68 k m h

Passo 3

Bom galerinha, nós estamos percorrendo uma distância d para chegar em São Paulo e depois mais uma distância d para voltar ao Rio, então a distância total da viagem será 2 d , tudo bem?

E quanto ao tempo nós faremos a mesma coisa que no passo 2, mas vamos usar as velocidades médias que achamos:

t = d 72,5 k m h + d 68 k m h

= 68 k m h d + 72,5 k m h d 4930 k m 2 h 2

= 140,5 k m h d 4930 k m 2 h 2

t = 140,5 d 4930 k m h

Na fórmula da velocidade:

v m é d i a = 2 d 140,5 d 4930 k m h

= 9860 k m h 140,5

= 70,2 k m h

v m é d i a ≈ 70 k m h

Passo 4

Para responder a letra (d) devemos estar atentos a diferença entre velocidade média escalar e velocidade média, tudo bem?

A velocidade escalar média é a razão entre a distância percorrida e o tempo, já a velocidade média é a razão entre o deslocamento e o tempo.

Como o carro volta para seu ponto de origem seu deslocamento é zero, não é? Se não há deslocamento, não há velocidade !!

Portanto, v m = 0 !!

Passo 5

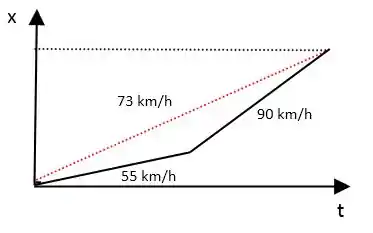
A velocidade média do caso (a) pode ser encontrada pela inclinação da reta que liga o ponto inicial ao final, em um plano cartesiano x por t .

Bem legal, não foi?

Resposta

a) v e m 1 = 73   k m / h

b) v e m 2 = 68   k m / h

c) v e m ' = 70   k m / h

d) v m = 0

e)

Exercícios de Livros Relacionados

Em uma corrida de 1k m , o corredor 1 da raia 1 ( com o tempo de 2m i n , 27,95s ) parece ser mais rápido que o corredor 2 da raia 2 ( 2m i n ,28,15s ). Entretanto, o comprimento L 2 da raia 2 pode se
Os morcegos se localizam pelo eco, na determinação da distância que os separa de objetos que não podem ver direito no escuro. O tempo entre a emissão de um pulso de som de alta frequência (um clique)
Em uma corrida de 1k m , o corredor 1 da raia 1 ( com o tempo de 2m i n , 27,95s ) parece ser mais rápido que o corredor 2 da raia 2 ( 2m i n ,28,15s ). Entretanto, o comprimento L 2 da raia 2 pode se
Você dirige do Rio a São Paulo metade do tempo a 55k m / h e a outra metade a 90k m / h . Na volta, você viaja metade da distância a 55k m / h e a outra metade a 90k m / h . Qual é a velocidade escala
A distância percorrida, até parar, por um carro esportivo que está a 200 km/h quando o piloto pisa no freio é 170 m. Supondo que a aceleração se mantém constante, determine o módulo da aceleração (a)