Oscilações Forçadas e Ressonância
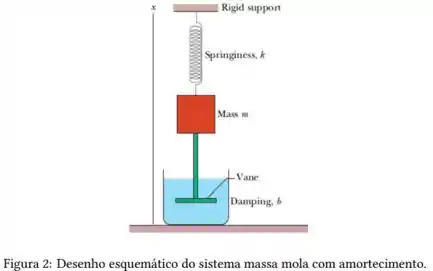
Considere a equação da amplitude de oscilação do sistema mostrado na figura abaixo,
Onde é a amplitude constante de uma força oscilatória externa de frequência . Qual é a amplitude de oscilação e a velocidade máxima do objeto quando excitado na frequência de ressonância?
- e
- e
- e
- e
- e
Passo 1
Se o sistema estiver oscilando na frequência de ressonância, , logo:
Passo 2
Bom, o sistema pode ser descrito como:
Logo, a velocidade é:
Essa função terá um máximo quando a função seno tiver seu máximo, ou seja, quando valer 1.Logo:
Sendo que seu módulo vale:
Resposta
d)
Exercícios de Livros Relacionados
13.21P Um carro sem carga tem massa de 1200kg . Quando dois passageiros, com massa-conjunta de 150kg , entram no carro, sua plataforma sofre um deslocamento de 3,0cm para baixo. O carro, com seus pass
Um corpo de 2,00k g oscila preso a uma mola que tem uma constante de força igual a 400N / m . A constante de amortecimento linear vale b = 2,00k g / s . O sistema é exictado por uma força senoidal de
Um oscilador linearmente amortecido perde 2,00 por cento de sua energia em cada ciclo. (a) Qual é o seu fator Q ? (b) Se sua frequência de ressonância é 300H z , qual é a largura da curva de ressonânc
Suponha que, na Eq. 15-45, a amplitude x m é dada por: x m = F m m 2 ω d 2 - ω 2 2 + b 2 ω d 2 1 / 2 onde F m é a amplitude (constante) da força alternada externa exercida sobre a mola pelo suporte rí
Neste problema, você deve deduzir a expressão para a potência média desenvolvida por uma força de excitação sobre um oscilador forçado.Mostre que a potência instantânea desenvolvida pela força de exci