Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Regime Transitório, Permanente e Ressonância

Ver Teoria
Exercício 4012345678910111213141516171819202122232425262728293031323334353637383941424344

Enunciado

Oscilações Forçadas e Ressonância

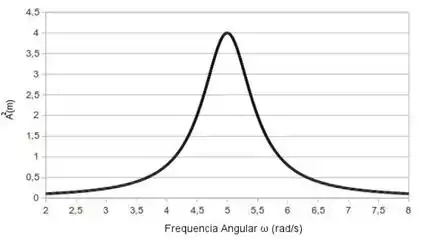
O gráfico abaixo mostra o quadrado da amplitude, A 2 ( ω ) , em função da frequência de oscilação de uma força senoidal aplicada. Dado que o sistema é fracamente amortecido, obtenha seu fator de qualidade, Q .

  1. Q = 1
  2. Q = 4
  3. Q = 10
  4. Q = 2
  5. Q = 5

Passo 1

Aqui vamos ter que usar a expressão:

A 2 ω = F 0 2 m 2 ω 0 2 - ω 2 2 + γ 2 ω 2

E o nosso fator de qualidade é dado por:

Q = ω 0 γ = ω 0 ∆ ω  

Onde ∆ ω é a largura de banda. Pra encontra-la, vamos tomar no gráfico os valores de ômega para A 2 2 , onde A é a amplitude máxima.

Sendo assim, precisamos descobrir ω 0 e γ pra calcular esse fator.

Só que, pelo gráfico, a gente descobre que ω 0 = 5 . Por que? Porque ali acontece a ressonância... Lembra que na ressonância o valor da frequência tende a ω 0 ?

Então, na ressonância nós temos: ω = ω 0 .

Logo, ω 0 = 5

Basta agora a gente encontrar o γ .

Passo 2

Pelo gráfico, vemos que: A 2 = 4 m . (amplitude máxima)

Então, para A 2 2 = 2 m . Olhando os valores de ômega que cruzam o gráfico para esse valor, vemos que:

ω 1 = 4,5 r a d / s

ω 2 = 5,5 r a d / s

Assim, a banda valerá:

∆ ω = 5,5 - 4,5 = 1,0 r a d / s

Passo 3

Logo, o γ pode ser calculado:

Q = ω 0 ∆ ω = ω 0 γ

∴

γ = ∆ ω = 1 r a d / s

Assim, o fator de qualidade pode ser calculado:

Q = ω 0 γ = 5 1 = 5  

Resposta

e)

Exercícios de Livros Relacionados

13.21P Um carro sem carga tem massa de 1200kg . Quando dois passageiros, com massa-conjunta de 150kg , entram no carro, sua plataforma sofre um deslocamento de 3,0cm para baixo. O carro, com seus pass
Um corpo de 2,00k g oscila preso a uma mola que tem uma constante de força igual a 400N / m . A constante de amortecimento linear vale b = 2,00k g / s . O sistema é exictado por uma força senoidal de
Um oscilador linearmente amortecido perde 2,00 por cento de sua energia em cada ciclo. (a) Qual é o seu fator Q ? (b) Se sua frequência de ressonância é 300H z , qual é a largura da curva de ressonânc
Suponha que, na Eq. 15-45, a amplitude x m é dada por: x m = F m m 2 ω d 2 - ω 2 2 + b 2 ω d 2 1 / 2 onde F m é a amplitude (constante) da força alternada externa exercida sobre a mola pelo suporte rí
Neste problema, você deve deduzir a expressão para a potência média desenvolvida por uma força de excitação sobre um oscilador forçado.Mostre que a potência instantânea desenvolvida pela força de exci