Oscilações Forçadas e Ressonância, MHA
Um circuito eletrônico é formado por uma resistência elétrica, , por uma indutância, , por um capacitor, e por uma fonte alternada . A equação diferencial para a corrente elétrica, é
o que se mostra que o circuito se comporta como um oscilador harmônico forçado e amortecido.
- Qual a frequência angular natural de oscilação da corrente, e o parâmetro de amortecimento, ?
- Sendo
- Para , escreva a solução geral da equação diferencial dada acima.
- Se as condições iniciais são e , determine a solução específica para este oscilador.
a solução estacionária, determine faça um esboço do gráfico de em função de .
Passo 1
Vamos comparar a equação
Com a equação de um oscilador forçado:
Fazendo a comparação, a gente tira que:
E :
Passo 2
b):
Vamos usar aqui a expressão:
Só que com as analogias certas. Ou seja, , . Além disso, vamos comparar de novo as equações:
E:
Percebemos que:
Aplicando todos esses valores na equação:
Legal! Bom, essa equação segue o padrão da outra, então também vai ser uma variação que terá um máximo na ressonância, ou seja, quando . O gráfico da curva vai ser: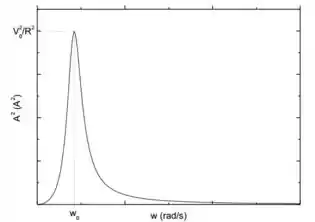
Passo 3
c):
Esse é o caso em que o amortecimento é subcrítico. Então a solução do sistema vai ser do tipo:
A gente sabe, da nossa teoria, que o modelo da solução homogênea pra um MHA em regime subcrítico é:
Onde
Fazendo a analogia com
Usamos um pra não causar confusão com da “força” externa.
Esse vale:
E a solução particular é do tipo:
Com e a serem determinados pelas condições iniciais( Assim como e da homogênea).
Logo:
Passo 4
d):
Parar :
Derivando a expressão em relação ao tempo:
Logo:
Substituindo o valor de
Arrumando essa bagunça:
Pronto! Achamos duas das constantes que precisávamos. A solução fica, então, em função de .
Resposta
a):
b):
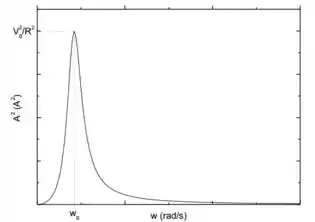
c):
d):