Dado um sistema de duas partículas de massa ligados por três molas de constante elástica e massa desprezível, como ilustrado abaixo:
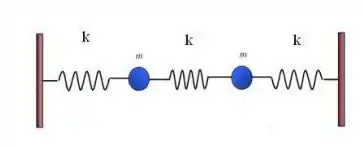
O sistema possui dois modos normais de vibração, e , onde . Quando o sistema oscila com frequência ou , a frequência de oscilação do centro de massa é respectivamente
- e
- e
- e
- e
- e
Passo 1
Precisamos primeiramente os modos de vibração dessas massas e a partir disso calcular o deslocamento do centro de massa por meio de
Então vamos ver esses modos!
Passo 2
Primeiro vamos escrever a segunda lei de Newton para as duas massas
Onde e são os deslocamentos das massas e em relação às suas posições de equilíbrio (e não a posição em si, como a gente tá acostumado).
Cada uma dessas massas estará em um MHS, assim podemos escrever
E calculando
E temos a mesma coisa para a massa 2
De forma que o nosso sistema de equações fica
E dando uma ajeitadinha
Que de forma matricial fica
Normalmente a gente calcularia o determinante dessa matriz e acharia os autovalores e depois os autovetores, mas o enunciado já nos deu os autovalores! Agora então ficou chuchu beleza!
Passo 3
-
Se lembrarmos da teoria de OHS que , então a gente fica com que
Que na nossa matriz fica
E na nossa equação matricial
De forma que a gente conclui que
Ou seja, as duas massas se deslocam de forma igual, quando uma vai para direita a outra vai para direita também por exemplo.
O deslocamento do nosso centro de massa (lá do passo 1) é dado então por
Como a massa oscila com frequência então o centro de massa vai oscilar com frequência também!
Passo 4
-
Como , então
Que na nossa matriz fica
E na nossa equação matricial
De forma que a gente conclui que
Ou seja, as duas massas se deslocam de forma oposta, quando uma vai para direita a outra vai para esquerda e vice-versa.
O deslocamento do nosso centro de massa (lá do passo 1) é dado então por
Ou seja, o centro de massa ficará paradão! O que faz sentido já que as duas massas se deslocam em sentidos opostos! A sua frequência de oscilação será .
Resposta
e)