Calcule
na região mostrada na figura abaixo,
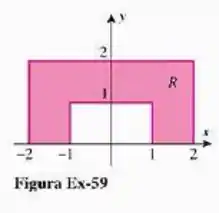
Passo 1
Opa, turubom??
Vamos começar escrevendo essa região, ok? Para isso, vamos dividí-la em partes:
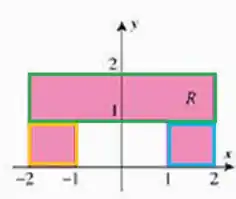
Chamando o retângulo verde de , o amarelo de e o azul de , temos que a integral da área que a gente quer, é a soma dessas três áreas coloridas!
Passo 2
Agora, vamos encontrar os inter valos de cada integral, de acordo com a imagem.
Para o retângulo verde, temos:
Para o amarelo:
Para o azul:
Passo 3
Aplicando o Teorema de Fubini, temos:
Repare que a ordem dos intervalos está de acordo com a ordem dos diferenciais!
Passo 4
Agora, vamos começar resolvendo a integral de :
Vamos começar fazendo a integral de dentro, essa daqui
Nesse caso, pode ser considerado como constante, então temos
Então essa integralzinha fica
Que dá zero 😊
Passando isso para integral de fora, temos
E a integral de zero é
Vamos guardar esse resultado que mais tarde a gente vai usar ele hehe
Passo 5
Calcular a integral de :
Vamos começar fazendo a integral de dentro, essa daqui
Nesse caso, pode ser considerado como constante, então temos
Então essa integralzinha fica a mesma da anterior, mas com outros limites de integração
Então vamos pegar esse e colocar na integral de fora! Fazendo isso ai, temos:
E essa nossa integral fica
Substituindo esses valores em temos
Que, podemos cortar os e simplificar em:
Então temos:
Vamos segurar esse resultado também!
Passo 6
Calcular a integral de :
Vamos começar fazendo a integral de dentro, essa daqui
Nesse caso, pode ser considerado como constante, então temos
Então essa integralzinha fica a mesma da anterior, mas com outros limites de integração
Então vamos pegar esse e colocar na integral de fora! Fazendo isso ai, temos:
E essa nossa integral fica
Substituindo esses valores em temos
Que, podemos cortar os e simplificar em:
Então temos:
Vamos segurar esse resultado também!
Passo 7
Ufaaa! Terminamos essas mini áreas, mas lembra laaa do começo que:
E achamos nos passos anteriores que
Então nossa integral de fica: