Em um determinado shopping do Rio de Janeiro, queremos saber se os gastos médios de duas lojas com o mesmo perfil podem ser considerados estatisticamente idênticos.
Tomou-se uma amostra de 12 clientes da loja “A” e de 10 clientes da loja “B”, obteve-se as seguintes estimativas:
Pede-se:
- Encontre o Intervalo de confiança para a diferença das médias da loja “B” para a loja “A” ao nível de confiança de 99%. Pelo resultado temos evidência para afirmar se existe diferença estatisticamente significativa entre os gastos médios da loja “B” para a loja “A”?
- Teste a hipótese de existir ou não diferença entre a variância dos gastos da loja “A” () e a variância dos gastos da loja “B” (), ao nível de significância de 5%.
Mostre claramente o seu desenvolvimento para o teste de hipótese determinando: as hipóteses nula e alternativa, a estatística do teste e a decisão acompanhada de um gráfico da função de probabilidade da estatística do teste, indicando claramente as áreas de rejeição e de aceitação de .
Passo 1
a)
Lembrando que o IC para diferença entre duas médias de populações diferentes é dado por:
Onde:
Que é nossa “média ponderada” de variâncias!
Passo 2
Começando pelo :
Então:
Passo 3
Agora vamos calcular . Como foi pedido um nível de confiança de 99%:
E daí temos que:
E nosso grau de liberdade vai ser:
Procurando com esses parâmetros na tabela T de Student temos que:
Passo 4
Agora juntando tudo que temos na fórmula do IC:
Reparem que a ordem que botamos dentro da fórmula respeita a ordem da diferença pedida no enunciado! Substituindo todos os valores:

Passo 5
b)
Agora vamos fazer um teste de hipótese da diferença entre duas variâncias. Montando as hipóteses:
Teste para diferença entre variâncias bilateral!
Vamos ter que realizar o teste F de Fisher para decidir entre nossas hipóteses!
Passo 6
Começando calculando nosso :
Passo 7
E agora nosso , que no caso bilateral são:
Como :
E os graus de liberdade e serão:
Agora procuramos na tabela com 2,5% de área na cauda inferior:
E pra finalizar na tabela com 2,5% de área na cauda superior:
Passo 8
E no gráfico isso tudo fica:
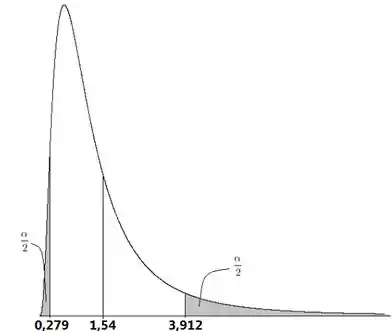
Ou seja, nosso caiu na região de aceitação! Então não rejeitamos , e temos evidências que não existe diferença entre as variâncias.