TAREFA da aula – 10 – Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 1
Uma máquina A produz peças circulares cujos diâmetros devem obedecer a uma determinada especificação em , e uma outra máquina B foi encontrada no mercado. Quer-se saber se os diâmetros médios das duas máquinas são semelhantes, ou seja, se as máquinas produzem peças que podem ser consideradas estatisticamente iguais em termos dos diâmetros delas.
Tomou-se uma amostra de peças da máquina A e peças da máquina B, tendo sido obtidas as seguintes estimativas amostrais:
Máquina A: e ;
Máquina B: e ;
a) Teste a hipótese se existe diferença entre a média dos diâmetros da máquina A () para a média dos diâmetros da máquina B (), ao nível de significância de .
b) Através do teste de hipótese para a variância, determine com o nível de significância de se existe diferença entre a variância dos gastos da máquina A () para a variância dos gastos da máquina B ().
Passo 1
Fala galerinha, bora fazer mais uma questão de PROBEST!!! É a última lista que tá faltando a gente resolver!
Nesse problema ele forneceu para gente as médias e desvios-padrão amostrais de peças produzidas por duas máquinas A e B. Para a máquina A com , obtivemos e . Já para a máquina B com , achamos e .
a) Nesse primeiro item, queremos saber se as duas médias são compatíveis entre si, dentro de uma significância de . Para comparar duas médias, usamos o teste para a variável:
A variável segue uma distribuição de Student para:
Eu sei que essas fórmulas são feias, mas é só usar elas direitinho e com calma que não vamos ter problema!
Passo 2
No fundo, o que queremos é fazer um teste de hipótese. Vamos estabelecer as hipóteses:
Se as médias forem compatíveis, a hipótese será aceita. Note também que se trata de um teste bilateral, como mostrado a seguir:
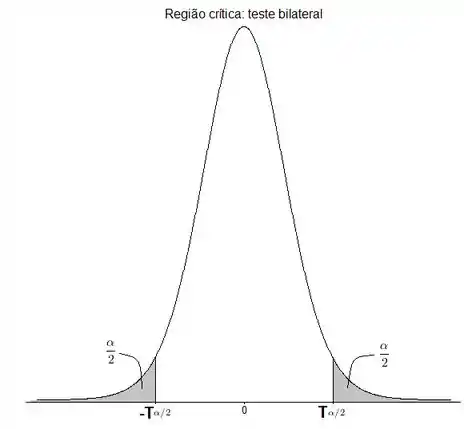
Assim, queremos a probabilidade de que a região central corresponda a e a porcentagem da região externa seja . Como a distribuição é simétrica e o teste é bilateral, dividimos essa porcentagem em partes iguais nas duas extremidades. Nosso objetivo é achar .
Para isso, olhamos na tabela na distribuição de Student. O primeiro passo para isso é calcular o número de graus de liberdade . Substituindo na expressão que escrevi acima:
Vamos arredondar para pois a tabela só apresenta valores inteiros. Queremos que
Olhando na tabela:
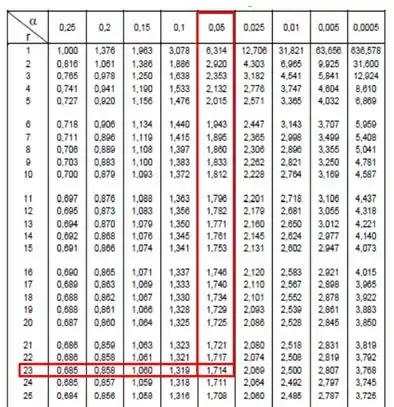
Portanto,
Passo 3
Como o teste é bilateral, nós vamos aceitar se...
Para calcular o fazemos na expressão para (já que essa é a hipótese que queremos testar). Fazendo isso,
É fácil ver que a condição é satisfeita, de modo que a hipótese deve ser aceita. Isso significa que as médias são compatíveis entre si!
Resposta
a) As médias são compatíveis entre si.