Um grupo de indústrias de alimentos pediu a pessoas que estimassem o número de calorias em cada um de tipos comuns de alimentos. Na tabela a seguir estão as estimativas médias das calorias atribuídas pelo grupo , o valor correto de calorias e o erro relativo :
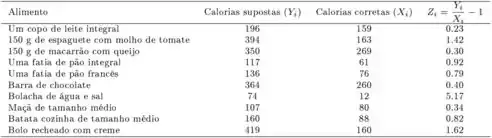
Dados: ; ; Desvios padrão: ; ; . Considere as seguintes assertivas:
- Existem valores de que podem ser considerados outliers (segundo o critério: valores superiores a ou inferiores a ).
- Não existem valores de que podem ser considerados outliers.
- Os limites dos intervalos de confiança da média das calorias supostas com de confiança são
- Os limites dos intervalos de confiança da média do erro relativo a de confiança são após a exclusão dos outliers.
- A dispersão dos erros é maior para valores menores que a mediana.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉

Para essa questão, foi dado uma tabela que contém valores de calorias supostas e calorias corretas e também foram feitas algumas afirmações a respeito dessa tabela.
O que temos que fazer é julgar essas afirmativas e descobrir quais estão corretas e quais estão erradas.
Foram dados alguns dados como: ; ; Desvios padrão: ; ; .
Vamos julgar um termo de cada vez para no fim descobrir qual afirmativa está correta e selecionar a resposta.
A afirmação diz que: “Existem valores de que podem ser considerados outliers (segundo o critério: valores superiores a ou inferiores a ).”
Este método de análise consiste em organizar o espectro amostral em ordem crescente e dividi-lo em 4 partes iguais. Vamos verificar se essa informação está correta. Primeiro vamos organizar os dados do espectro amostral.

Com o espectro a mostrar organizado vamos verificar se os valores superiores e inferiores são extrapolados.
Vamos calcular o valor superior:
Só pelo cálculo do valor superior vemos que o limite é extrapolado, já que o maior valor da nossa amostra é e o limite superior é , portanto, a afirmativa é verdadeira.
Passo 2
A afirmação diz que: “Não existem valores de que podem ser considerados outliers.”
Essa afirmação é falsa já que acabamos de provar que existem valores que são considerados outliers.
A afirmação diz que: “Os limites dos intervalos de confiança da média das calorias supostas com de confiança são ”
Pra verificar essa informação vamos utilizar a fórmula do intervalo de confiança, onde
Primeiro precisamos calcular a média das calorias supostas, pra isso foi dado , logo a média pode ser obtida como
Também precisamos calcular o grau de Liberdade para verificar qual índice vamos utilizar na equação
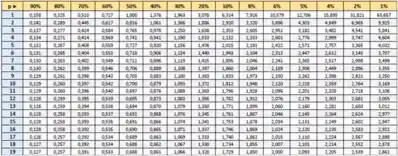
Vemos na tabela como , logo
O grau de Liberdade é calculado como
Com essas informações vendo vemos que na linha com o grau de Liberdade e a coluna de , o que vamos usar é .
Substituindo esses valores na fórmula do intervalo de confiança, temos
Vemos que o intervalo de confiança que encontramos é diferente do intervalo de confiança da dada na afirmação portanto a afirmação está incorreta.
Passo 3
A afirmação diz que: “Os limites dos intervalos de confiança da média do erro relativo a de confiança são após a exclusão dos outliers.”
Essa formação é bem completa já que para prova-la vamos primeiro calcular os limites outliers, descobrir quais amostras estão fora desse limite, exclui-los do espectro amostral e calcular o intervalo de confiança.
Primeiro passo: Calcular os limites outliers.
Já organizamos nosso espectro amostral e vamos calcular o limite inferior do intervalo outlier.
O valor inferior é dado como
Com isso vemos que temos apenas um valor fora do limite, excluindo-o do nosso espectro amostral, temos
![]()
Também precisamos calcular a média das amostras que sobraram no nosso espectro
Neste caso, temos que utilizar outra tabela de valores de

Onde .
Substituindo as informações que temos na equação do intervalo de confiança
Com isso vemos que a afirmativa é verdadeira
Passo 4
Por fim a afirmativa diz que: “A dispersão dos erros é maior para valores menores que a mediana”
Para verificar essa informação vamos calcular o desvio padrão dos valores abaixo da mediana e o desvio padrão dos valores acima da mediana.
Para os valores abaixo da mediana:
Para valores acima da mediana:
Por fim vemos que o desvio padrão para os valores maiores que a mediana é maior que o desvio padrão para os valores menores que a mediana, portanto a afirmação está incorreta.
Como apenas as informações e estão corretas a alternativa correta é a letra B
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
B) As assertivas e estão corretas