Tarefa da aula – 9 – Probabilidade e Estatística (ENG1029) – 2020/2 – Questão 3
A tabela a seguir mostra a estatística descritiva do desempenho acadêmico de duas turmas (T1 e T2) durante o curso de PROBEST na PUC-Rio.
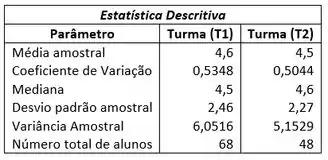
Os alunos da turma T1 afirmam que em média o desempenho deles é muito melhor quando comparado com o desempenho dos alunos da turma T2. Por outro lado, os alunos da turma T2 afirmam que apesar do valor médio da T1 ser um pouco maior, ambos os desempenhos podem ser considerados estatisticamente iguais. Para resolver esta discussão, pede-se que você apresente uma solução detalhada das seguinte questão: Estime o intervalo de confiança para a diferença das médias populacionais das turmas (T2 – T1) para um nível de confiança de 99%. Considerando o resultado obtido, qual a sua conclusão? Deduzir detalhando todos os passos necessários para a construção do Intervalo de confiança – IC.
Passo 1
Bom! Bora lembrar da fórmula do para diferença de médias:
Onde esses caras com as barrinhas em cima são nossas queridas médias amostrais, e o é:
Vamos por partes relembrando o que cada um desses caras aí é, e calculando o valor deles.
Passo 2
O nível de confiança pedido foi de , então:
Esse aí é nosso nível de significância. Com ele, podemos descobrir quanto vale o nosso termo T de Student da fórmula:
Beleza, esse é um dos parâmetros que precisamos conhecer para usar a tabela. O outro, é o grau de liberdade, que é dado por:
Onde e são os tamanhos das nossas duas amostras, ou seja, o número total de alunos em cada uma das duas turmas:
Agora conhecemos nossos dois parâmetros e podemos usar a tabela T de Student. Ela dá pra gente que:
Se sua tabela não tiver o número exato de graus de liberdade, o valor dele pode ser aproximado para o número de graus de liberdade mais próximo do que queremos!
Passo 3
Agora vamos calcular o , que nada mais é que um estimador da combinação dos dois desvios padrões das nossas amostras. Ele é dado por:
Como vimos, e são os tamanhos das amostras, e e vão ser os desvios padrões amostrais de cada turma. Substituindo os valores dados na tabela na fórmula:
Com isso podemos calcular :
Então nosso fica: