Uma bola é lançada sob um ângulo de . A que altura se encontra depois de percorrer em linha reta?
Passo 1
Falaaaaa Aí!! Antes de qualquer coisa vamos entender o que o exercício está pedindo?? No exercício é dito que uma bola é lançada sob um ângulo de . Ou seja,
Beleza?! Precisamos encontrar a altura que a bola vai se encontrar após percorrer em linha reta, ou seja
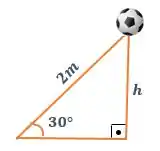
Queremos então encontrar o valor da altura !! Show de bola?!

Passo 2
Se observarmos bem o triângulo, nós temos um ângulo de e a medida que queremos encontrar está “de frente” para o ângulo de , concorda?
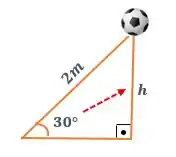
Ou seja, a medida é o cateto oposto ao ângulo de . Beleza?!
Além disso, temos a medida do lado que está de frente para o ângulo de , que é chamada de hipotenusa!
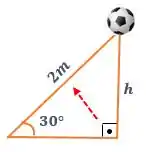
Como estamos trabalhando com a medida do cateto oposto e da hipotenusa , então a razão trigonométrica mais adequada que envolve o cateto oposto e a hipotenusa é o . Assim, precisamos calcular o !
Passo 3
Sabemos que o
Certo?! Aplicando essa fórmula para o , temos
Beleza?!
Passo 4
Agora precisamos ver qual é o valor de . Para isso, basta olharmos para a nossa querida tabelinha!
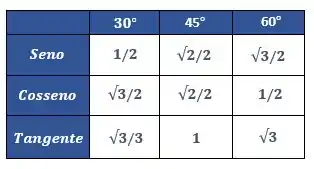
Agora é só procurar o valor do
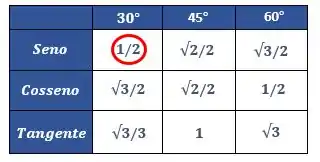
E substituir na nossa equação
E isolar o !!! Para isso, vamos multiplicar cruzado
Agora passamos o pro outro lado da igualdade dividindo
Assim,
Ou seja, a altura que a bola se encontra depois de percorrer em linha reta é de !
Beleeeza?!

Resposta
A altura que a bola se encontra depois de percorrer em linha reta é de !