Uma pessoa, sobre uma colina, avista um prédio de 100 m. O segmento ligando seus olhos ao topo
do prédio e à base do prédio formam ângulos de 18◦ e 14◦, respectivamente. Determine a distância (horizontal) entre a pessoa e o prédio.
Passo 1
Fala galera, tudo beleza? Vamos para mais uma questão de matemática básica! Vamos fazer um desenho da situação descrita
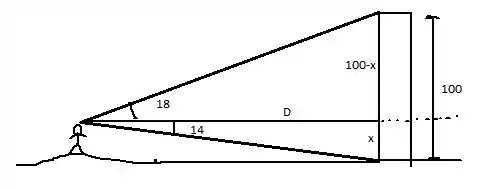
Ou seja, podemos usar os ângulos e a altura para descobrirmos a distância até o prédio.
Seja essa distância. Então temos que:
Podemos calcular as tangentes e teremos:
Podemos fazer a seguinte substituição:
Passo 2
Agora precisamos isolar o :

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊