Uma pessoa de 1,65 m de altura observa o topo de um edifício conforme o esquema abaixo.
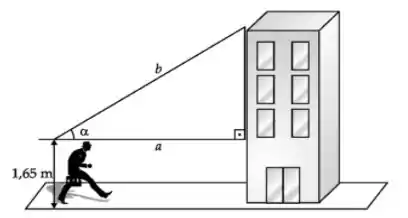
Para sabermos a altura do prédio, devemos somar a:
Passo 1
Falaaaaa Galeeera!! Beleza?! Vamos analisar o desenho com um pouco mais de calma?? Vamos fazer um esboço mais simples para nos ajudar!
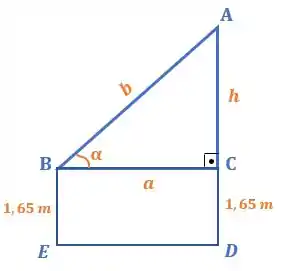
Se você reparar, o segmento que vale representa a altura da pessoa, certo?! Como o triângulo formado na imagem é retângulo, então o segmento CD também mede 1,65 metros. Beleza?!
Então vamos lá, se você reparar, o triângulo é retângulo. Perceba que a altura do prédio é igual a soma dos segmentos e . E como podemos encontrar o valor do segmento ?
É o que veremos agora!!
Passo 2
Para calcularmos o valor do segmento podemos utilizar uma das razões trigonométricas: ou . Lembrando que é a razão entre cateto oposto, ou seja:
O cateto oposto na nossa imagem é a medida do lado oposto ao ângulo , ou seja, . Já a hipotenusa é a medida do lado oposto ao ângulo de , ou seja, . Assim,
Isolando a altura que é o valor que queremos encontrar, temos
Essa é a nossa letra (e)!
Resposta
Letra E