Calcule o valor de no triângulo abaixo:
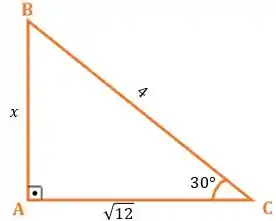
Passo 1
Opaaa! Fala Aí!! Queremos encontrar o valor de , certo? Como podemos fazer isso???

Antes de mais nada, se você reparar, nós temos os valores de dois lados do triângulo retângulo e também temos o valor de um ângulo do triângulo . Certo?
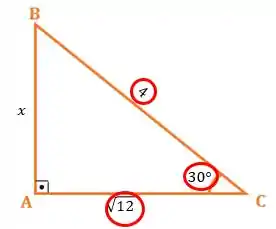
Por isso, vamos utilizar uma das razões trigonométricas para encontrar o valor de ! Sempre que estivermos trabalhando com medidas dos lados de um triângulo retângulo e ângulo, podemos utilizar as razões trigonométricas para facilitar nossa vida!

Então como vai funcionar?????? É o que veremos agora!
Passo 2
Se observarmos bem o triângulo, nós temos um ângulo de e a medida que queremos encontrar está “de frente” para o ângulo de , concorda?
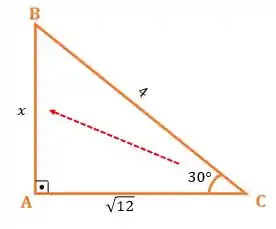
Ou seja, a medida é o cateto oposto ao ângulo de . Beleza?!
Além disso, temos a medida do lado que está de frente para o ângulo de , que é chamada de hipotenusa!
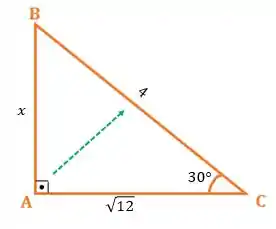
Como estamos trabalhando com a medida do cateto oposto e da hipotenusa , então a razão trigonométrica mais adequada que envolve o cateto oposto e a hipotenusa é o . Assim, precisamos calcular o !
Passo 3
Sabemos que o
Certo?! Aplicando essa fórmula para o , temos
Beleza?!
Passo 4
Tá... mas e agora?

Agora precisamos ver qual é o valor de . Para isso, basta olharmos para a nossa querida tabelinha!
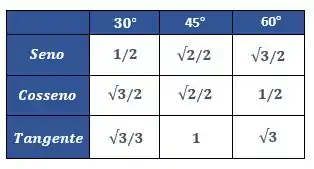
Agora é só procurar o valor do
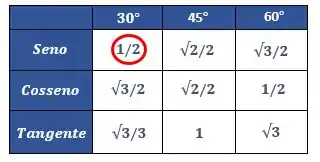
E substituir na nossa equação
E isolar o !!! Para isso, vamos multiplicar cruzado
Agora passamos o pro outro lado da igualdade dividindo
Assim,
Beleeeza?!
