Cada um de dois longos solenoides coaxiais é percorrido por uma corrente elétrica estacionária, de mesma intensidade , porém com sentidos contrários. Ambos os solenoides têm o mesmo comprimento , sendo que o interno possui raio e voltas, ao passo que o externo possui raio e voltas, sendo e .
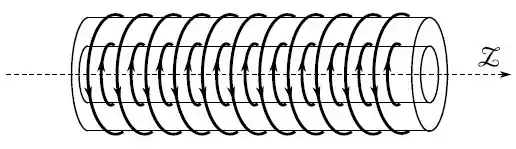
Sendo a distância até o eixo comum dos solenoides, e considerando o campo magnético fora dos dois solenoides igual a , podemos expressar o campo magnético dentro do solenoide interno e entre os dois solenoides , respectivamente, como
; .
; .
; .
; .
; .
Passo 1
O campo magnético gerado por um solenoide é dado por:
Utilizando a regra da mão direita, escrevendo separadamente o campo magnético gerado por cada solenoide, teremos:
Agora vamos olhar cada região separadamente:
- :
- :
Nessa região, temos tanto o campo magnético gerado pelo solenoide externo, quanto pelo interno, logo:
Para essa região, consideraremos apenas o campo magnético gerado pelo solenoide externo. Isso acontece porque, na região fora de um solenoide, consideramos o campo magnético nulo, logo, como essa região está no exterior do solenoide interno, não vamos considerar o campo magnético gerado por ele.
Portanto:
A resposta certa é a letra .
Resposta
; .