Um solenoide toroidal, mostrado na figura e em corte transversal na figura , contém espiras e é percorrido por uma corrente . O núcleo do solenoide está preenchido por ar .
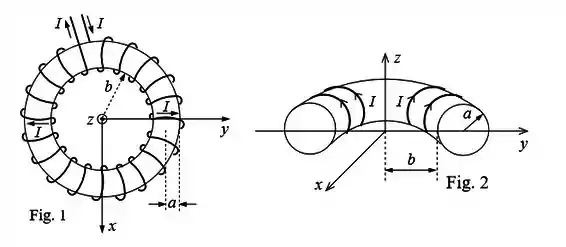
(a) Calcule o vetor campo magnético em coordenadas cartesianas isto é na forma ao longo do eixo para .
(b) Constrói-se um outro solenoide toroidal com as mesmas dimensões do solenoide da figura mas com um núcleo de aço inoxidável de permeabilidade . Passando a mesma corrente pelos dois solenoides, calcule a relação entre o número de espiras e no solenoide com núcleo de aço e com núcleo de ar, respectivamente, para produzir o mesmo campo magnético nos núcleos dos dois solenoides.
Passo 1
a) Sabemos que o solenoide toroidal da figura 1 possui simetria esférica, portanto:
Usando a lei de Ampère com um caminho circular de raio , conforme a figura, obtemos
Sobre o eixo , o campo magnético aponta para baixo, ou seja, na direção
Sabendo que este resultado vale somente para (dentro do solenóide), para ou (fora do solenoide), a corrente total e então:
Organizando os resultados então, agora em função de , como foi pedido:
Passo 2
(b) O campo dentro do solenoide com núcleo de aço é , ou seja, basta substituir por na expressão do item (a).
Como queremos o caso que , obtemos
Resposta
a)
b)