Um solenóide toroidal possui um raio interno e raio externo . O solenoide possui espiras e conduz uma corrente de . Qual é o módulo do campo magnético em um ponto cuja distância ao centro do toróide é:
- 12,0 cm?
- 16,0 cm?
- 20,0 cm?
Passo 1
Você viu aqui com a gente que o campo magnético produzido por um toróide com espiras pelas quais passa uma corrente é dado por
sendo que é o raio médio do toróide, como você pode visualizar na figura abaixo (deixa a sua imaginação fluir agora para enxergar espiras enroladas muuuuito juntas umas das outras...kkk Conseguiu? ):
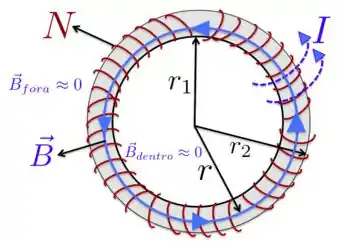
O campo magnético produzido pelas correntes das espiras produz um campo magnético no interior do toróide, com sentido e direção indicados na figura acima. Se a espessura do núcleo do toróide for pequena comparada com o valor do raio médio , ou seja, , então o campo magnético é aproximadamente uniforme no interior do toróide, e tem o valor dado pela expressão acima, e os campos resultantes dentro, , e fora, , são aproximadamente NULOS. Geralmente, a gente fala só que é IGUAL A ZERO mesmo, sem dizer, na maioria dos problemas, a palavra “aproximadamente”, tranquilo?
Passo 2
a) No caso deste item, fica moleza, né? Dá uma olhada lá e repara que a distância que é considerada para este item é . Isso significa, como você consegue ver direto da figura agora, que o campo magnético nesse caso é
Passo 3
b) Já para , a gente acabou de ver que o campo, nas condições que mostrei pra você, tem praticamente o mesmo valor em todos os pontos do interior do toróide e você já viu e sabe agora que o campo lá dentro é
Tranquilo??
Passo 4
c) Agora com a figura que você tem aí em cima ficou molezinha demais resolver este item, né não? Dá uma olhada lá e veja que o campo magnético para , ou seja, fora do toróide é NULO!! Fechou, então! Checa lá na figura e veja que: