UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 4b
Considere um solenóide toroidal de raio médio , com seção transversal de área e voltas de fio enroladas de forma compacta ao longo de seu comprimento.
Suponha que o solenóide é fino, de forma que as dimensões de sua seção transversal sejam pequenas em comparação com . Assim, podemos dizer que o campo magnético é aproximadamente uniforme sobre a seção transversal e coincide com o valor calculado para . Nessas condições, determine a auto-indutância do sistema.
Passo 1
Eaew, tudo certinho com você?
O esquema que o enunciado descreve tem o seguinte formato
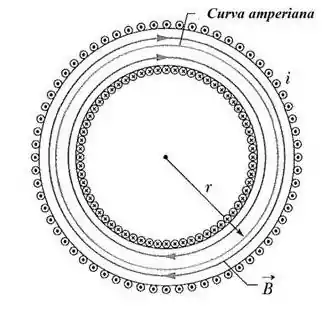
em que é o raio médio. A área transversal deste toróide é e temos que o fio dá voltas compactadas ao longo do toróide. A alternativa nos pede para que
Suponha que o solenóide é fino, de forma que as dimensões de sua seção transversal sejam pequenas em comparação com . Assim, podemos dizer que o campo magnético é aproximadamente uniforme sobre a seção transversal e coincide com o valor calculado para . Nessas condições, determine a auto-indutância do sistema.
Ou seja, temos um campo magnético uniforme da forma
em que usei o resultado da alternativa anterior com . Mas como determinamos a auto-indutância? Podemos lembrar que para um solenóide esta grandeza está relacionada ao fluxo do campo magnético pela seção transversal do próprio solenóide de forma que
Vamos calcular este fluxo!
Passo 2
Com o campo tem linhas de campo circulares e é uniforme, temos que ele cruza perpendicularmente as seções transversais do toróide, sendo assim, temos que o fluxo pode ser resumido como
e, portanto, a auto-indutância é dada por
A questão foi isso! Te vejo na próxima! Tchau Tchau!