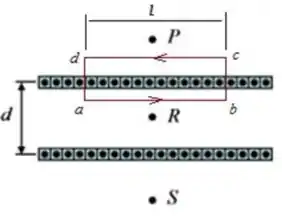
Condutores retilíneos longos, com seções retas quadradas, cada um deles conduzindo uma corrente estacionária com sentido para fora do plano da página, são colocados um ao lado do outro, formando duas placas finas que se estendem até o infinito, como mostrado na figura abaixo. Cada plano formado possui condutores por unidade de comprimento. Quais são, respectivamente, os módulos dos campos magnéticos produzidos nos pontos , e ?
(a), ,
(b), ,
(c), ,
(d), ,
(e), ,
Passo 1
Vamos considerar somente um plano primeiramente.
Temos que pela regra da mão direita o campo magnético tem que ser paralelo à plano, apontando para esquerda acima dele e para direita abaixo, conforme a figura
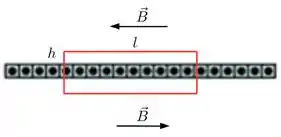
Assim, se calcularmos a circulação do campo magnético ao longo do caminho em vermelho temos
Lembrando que as integrais de caminho verticais são nulas, já que o campo é perpendicular ao deslocamento vertical.
Por outro lado, pela lei de Ampére
A corrente total dentro da nossa Amperiana é dada por
Já que é o número de condutores por comprimento
Assim
Passo 2
Beleza, agora vamos juntar os dois planos
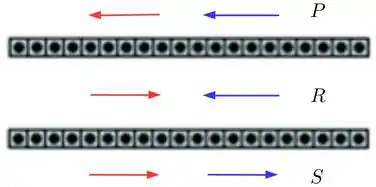
Em vermelho temos o campo gerado pelo plano de cima e em azul o campo gerado pelo plano de baixo.
Os campos gerados pelos dois planos têm mesma magnitudes, porém tem direções diferentes dependendo da região.
Na região entre os planos (região ), os campos de cada plano têm direções opostas, o que significa que o campo total é nulo
Na região superior (região ) os campos se somam, de forma que o módulo do campo nessa região é dado por
E na região inferior (região ) os campos se somam de novo (só que apontando para outro sentido) e o módulo nessa região será
Resposta
(a)