UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 1d
Um solenóide longo de raio é posicionado no interior de um segundo solenóide longo de raio , de forma que seus eixos sejam coincidentes com o eixo de um sistema de coordenadas cartesianas. O número de espiras por unidade de comprimento em cada solenóide vale e , respectivamente. Suponha que os solenóides podem ser tratados como infinitos e que o enrolamento dos fios é compacto. Quando conveniente, considere um segmento de solenóide de comprimento nas análises.
Suponha agora que o solenóide menor seja deslocado perpendicular ao seu eixo por uma distância . Determine a indutância mútua do sistema nessa nova configuração.
Passo 1
Eaew, belezinha?
Esse é um problema longo com várias alternativas, então vamos com calma, tudo bem? O enunciado começa nos apresentando dois solenóides coaxiais de raio e raio . O que isso quer dizer? Quer dizer que temos um solenóide dentro do outro, de forma que o campo magnético gerado por eles ao passarmos uma corrente elétrica estarão na mesma direção . Um solenóide é um objeto físico que pode ser representado da seguinte maneira
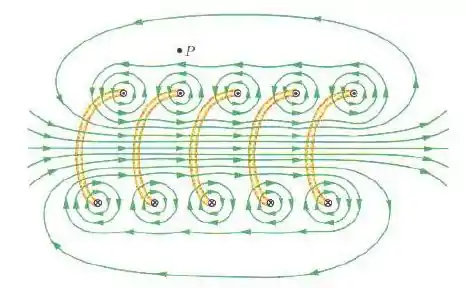
Os fios em amarelo são percorridos pela corrente, e as linhas de campo magnético em verde dependem do sentido em que essa corrente percorre (em nosso caso temos um desses solenóides dentro do outro). A intensidade do campo magnético depende intimamente da densidade de espiras por unidade comprimento, em nosso caso e , para o solenóide menor e maior respectivamente!
Esta alternativa nos pede
Suponha agora que o solenóide menor seja deslocado perpendicular ao seu eixo por uma distância . Determine a indutância mútua do sistema nessa nova configuração.
Como vimos na alternativa anterior, podemos escrever a indutância mútua por unidade de comprimento através da definição
em nosso caso, é mais conveniente utilizar a identificação
em que o índice maior e menor indicam sobre qual solenóide estamos falando! Lembre-se também que o fluxo no menor é devido a corrente no maior! Essa alternativa é uma pegadinha, e o segredo está no fato de que estes são solenóides longos! Note na figura acima que as linha de campo magnético dentro do solenóide são todas paralelas no limite que podemos desconsiderar os efeitos de bordas! Isso te dá alguma dica?
Bora lá!
Passo 2
O fato das linhas serem todas paralelas faz com que o fluxo sobre os solenóides não mude devido ao deslocamento perpendicular do solenóide interno (contando que o mesmo se mantenha dentro do solenóide externo, fato suportado pela afirmação que ), sendo assim, temos que a indutância mútua será a mesma obtida na alternativa anterior, dada por
A questão foi isso! te vejo na próxima! Tchau Tchau!