A porção superior da figura abaixo mostra parte de um toróide de seção retangular, de raio interno , raio externo e espessura . Tal toróide contém espiras conectadas, percorridas por uma corrente elétrica . Uma ilustração representativa da configuração geométrica de todo o toróide é dada na porção inferior da figura. Considere que a permeabilidade magnética do vácuo é dada por .
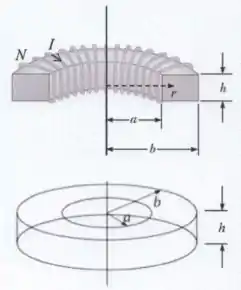
- Usando a lei de Ampère, calcule o módulo do campo magnético a uma distância do eixo de simetria que passa pelo centro do toróide, onde .
- Calcule o módulo do fluxo magnético através de uma das espiras retangulares do toróide.
- Calcule a energia magnética armazenada no interior de todo o toróide.
Passo 1
Vamos tentar entender a situação do problema olhando para a figura abaixo. Representamos apenas uma seção transversal de um toróide, neste caso apenas metade do toróide e apenas algumas das espiras retangulares. Cada uma dessas espiras transporta uma corrente , que circula no sentido horário indicado na figura.
Por isso, pela regra da mão direita, o campo magnético que essas correntes geram está entrando no plano da página. Para facilitar nossa discussão, colocamos também a área sempre paralela ao campo magnético , como ilustrado na figura. Colocamos também uma área infinitesimal pela qual o campo passará.
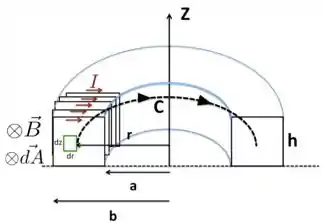
A corrente em cada uma das espiras atravessará uma área definida pelo contorno fechado , que está a uma distância do eixo . CUIDADO: agora estamos falando da área delimitada pelo contorno (nossa amperianda!), que é , e não de !! Repara que na figura mostramos apenas a metade dessa curva fechada para facilitar o entendimento da questão, mas imagina essa curva como um círculo de raio .
Passo 2
a) Para calcular o fluxo, precisamos do campo magnético produzido pelas correntes nas espiras. Para isso, vamos aplicar a lei de Ampère à nossa amperiana .
Utilizando a figura acima e também a regra da mão direita, vemos que o campo está entrando no plano da página e é sempre paralelo ao elemento da curva . Além disso, esse campo tem o mesmo valor sobre todos os pontos de , por isso podemos escrever o seguinte
onde é a corrente total que atravessa a área delimitada pela curva fechada . Se a gente olha a curva fechada de cima para baixo, “vamos enxergar” correntes atravessando a área do círculo . Por isso é que temos
Pegou essa ideia?
Então, continuando, obtemos o seguinte módulo para o campo magnético
No caso de um toróide ideal, esse campo magnético que encontramos fica todo concentrado na região e não há campo magnético que “vaza” para a região nem para .
Passo 3
b) Tendo o valor do campo gerado pela corrente que passa nas espiras, podemos encontrar o fluxo magnético através de uma espira retangular. Como o elemento de área é sempre paralelo a e este tem o mesmo valor em todos os pontos da amperiana , temos que
Aqui, não podemos tirar o campo magnético da integral, já que sua expressão depende da distância , como obtivemos no Passo 2. Por essa razão, não tem o mesmo valor em todos os pontos.
Agora, dá uma olhada lá na figura e repara que, neste sistema de coordenadas, o elemento infinitesimal de área atravessada pelo campo magnético é . Por isso, substituindo a expressão para que encontramos, o fluxo através de uma espira retangular é:
Resolvendo a integral acima, obtemos que o fluxo magnético através de apenas uma das espiras do toróide é:
Embora esse fluxo magnética dependa de , que é o número de espiras, é o fluxo através de uma única espira e esse que aparece aí é por causa do campo que as correntes produzem em .
Passo 4
c) Para encontrarmos qual é a energia armazenada no campo magnético no interior do toróide, precisamos calcular a sua autoindutância, já que temos a seguinte relação:
O problema nos informa , mas não sabemos ainda a expressão para . Então, para obter , vamos começar nossa solução pela expressão do fluxo magnético total e sua relação com a autoindutância de acordo com
sendo que é corrente que percorre cada uma das espiras retangulares do toróide.
Como o campo magnético fica todo concentrado dentro da região , o fluxo total do campo magnético é igual a vezes o fluxo através de uma única espira. Por isso, já usando a expressão que encontramos no final do Passo 3, teremos:
que nos dá a autoindutância
Com isso, fechamos a questão, uma vez que a energia total armazenada no campo magnético do torólide é: