UFRJ, Sem Campus, Física 3, Listas de Física 3 - UFRJ - Lista 9 - Indutância, Questão 6
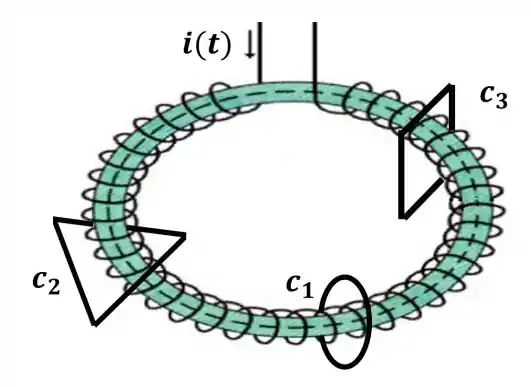
Considere um solenóide toroidal de seção transversal circular de raio . Ele é atravessado por uma corrente de intensidade que varia lentamente com o tempo. Considere também três espiras planas orientadas paralelamente às seções transversais do solenóide: , uma espira circular de raio , , uma espira triangular de lados iguais a e , uma espira quadrada de lado , dispostas no solenóide como mostrado na figura abaixo, envoltas e centralizadas no mesmo. Sejam , e as indutâncias mútuas entre o solenóide e as espiras , e , respectivamente, quando consideradas individualmente. Ordene , e de acordo com os seus módulos.
Passo 1
Oiie, tudo bem com você?
A figura resume bem o que o enunciado descreve
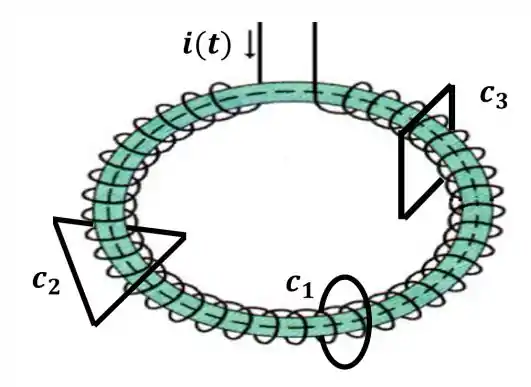
A corrente indicada varia lentamente e temos que as dimensões das três espiras, , e são indicadas como, uma circunferência de raio , um triângulo de lado e um quadrado de lado . A interação individual das espiras com o solenóide gera três indutâncias mútuas individuais, sendo elas e . Precisamos organizar as três em relação a seu módulo! Mas como obter este módulo? Vamos considerar que a interação é dada apenas entre o solenóide e as espiras individualmente, sendo assim, para cada par, temos que a indutância mútua será obtida pela relação
Essa relação, no entanto, nos indica uma questão conceitual que pode resolver a nossa questão imediatamente! Pense um pouco sobre a definição de fluxo, e vem comigo para o passo !
Passo 2
O segredo aqui está no fato que o campo magnético gerado pelo toróide só existe em seu interior, portanto, a área na qual existe fluxo do campo magnético é somente a área que é a seção transversal do toróide! De forma que para todas as espiras, temos o mesmo fluxo
nos três casos temos também que , e a corrente no toróide é sempre a mesma
Portanto, podemos garantir que
Independentemente das dimensões das três espiras! A questão foi isso! Te vejo na próxima! Tchau Tchau!