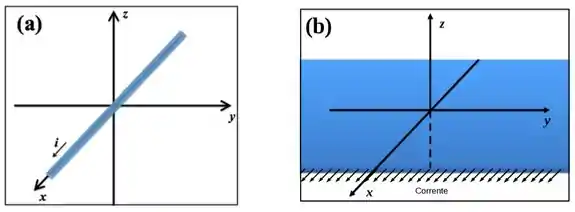
(a) Determine o módulo e descreva as linhas de campo do campo magnético gerado por um fio retilíneo longo conduzindo uma corrente ao longo do eixo (ver figura (a)).
(b) Considere agora uma chapa no plano , que podemos aproximar como infinita, conduzindo uma corrente na direção com densidade uniforme por unidade de largura (ver figura (b)). Utilizando o resultado da letra (a), deduza a direção e o sentido do campo magnético acima e abaixo da placa.
(c) Utilize o resultado do item (b) e a lei de Ampére para calcular o módulo do campo acima e abaixo da placa.
Passo 1
Pela regra da mão direita temos que o campo magnético apontará na direção , conforme a figura abaixo (feita pela nossa direção de arte)
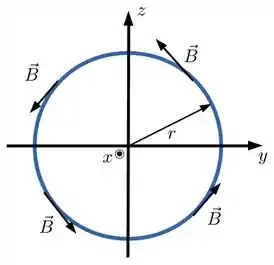
Como todas as direções são equivalentes, temos que o campo só pode depender da distância até o fio ou seja
Vamos escolher como amperiana o círculo de raio centrado na corrente. Temos que o módulo do campo é constante ao longo desse círculo e que ele sempre aponta na direção assim como o elemento infinitesimal de comprimento
Assim a circulação do campo magnético é dada por
Por outro lado temos a lei de Ampére
Assim
E o vetor campo magnético é dado por
Passo 2
Agora vamos ter fio a rodo passando uma corrente ! Melhor que um disso, só infinitos disso! Vamos ver o que acontece nesse caso!
Já vimos como é o campo devido a um fio. Antes de irmos para o caso de infinitos fios vamos para o caso de dois. Por que é assim que se conta: 1, 2 e infinito!
Vamos olhar para o campo em um ponto entre os dois fios com corrente cada
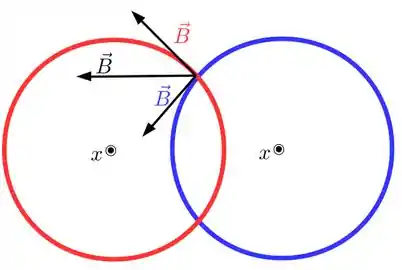
Temos que o campo nesse ponto apontará para a esquerda, pois é a soma dos campos de cada um dos fios. Se o ponto estivesse abaixo da linha que conecta os dois fios esse campo apontaria para esquerda pelo mesmo argumento.
Agora vamos considerar infinitos fios! No caso de infinitos fios, se estamos olhando para um ponto , sempre haverá para cada fio a uma dada distância a esquerda de um outro fio a essa mesma distância a direita de
Isso significa que podemos raciocinar com um conjunto de infinitos pares de fios cujo centro de cada par está logo acima ou logo abaixo de .
Como o nosso ponto não tem nada de especial (é genérico) temos que acima do plano de infinitos fios o campo aponta para esquerda () e que abaixo do plano o campo aponta para direita ().
Passo 3
Para calcular o módulo do campo usaremos a lei de Ampére.
A amperiana que usaremos é o retângulo a seguir
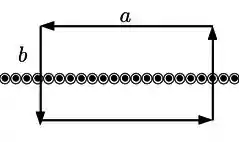
Como o campo é horizontal temos que a circulação do campo magnético é dada por
Já a corrente total dentro dessa amperiana vai ser dada por
Lembrando que é a densidade de corrente.
Assim pela lei de Ampére
Resposta
(a)
(b) Acima do plano campo aponta para esquerda () e abaixo do plano o campo aponta para direita ().
(c)