Se o peso do mastro é desprezível comparado à carga de aplicada, determine as forças trativas e nos cabos e a força atuando na rótula em .
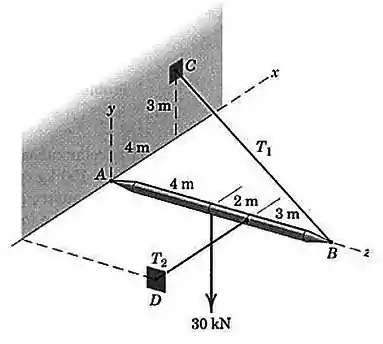
Passo 1
O diagrama de corpo livre fica assim:
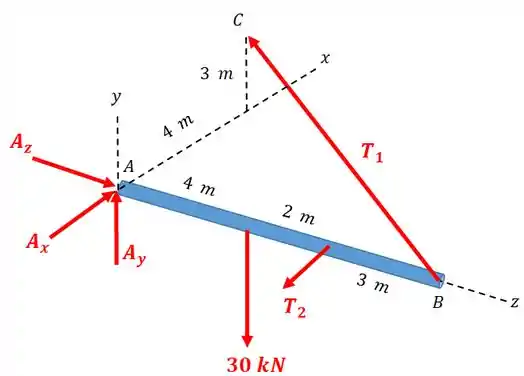
Passo 2
Temos que calcular a direção e sentido da força trativa que é dada pela reta que vai do ponto em direção ao ponto :
Temos que as coordenadas dos pontos e são:
E:
Então:
Então, o vetor normalizado fica:
Então, o vetor da força trativa fica:
Já o vetor é paralelo ao eixo , então podemos escrever:
Passo 3
Vamos começar calculando o momento em relação ao eixo :
Repare que somente a componente da força vai ter braço de alavanca com relação ao eixo :
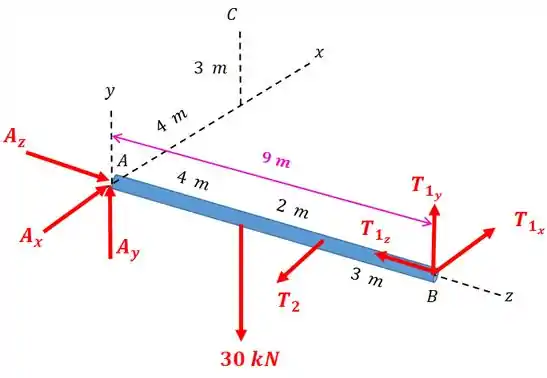
Então:
Passo 4
Agora vamos calcular o momento com relação ao eixo . As forças que exercem momento com relação a este eixo são:
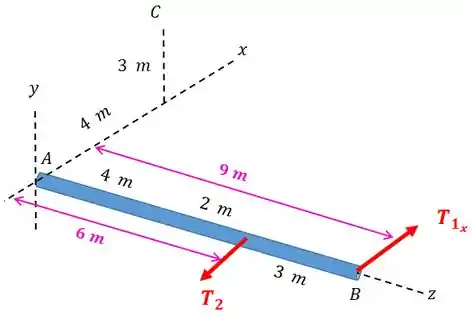
Então:
Passo 5
Para achar as reações de apoio, vamos fazer o somatório das forças:
Vamos ter que separar as equações de acordo com as componentes:
Então, a reação é:
A reação é:
E a reação fica:
Então, o vetor é:
E a resultante fica: