Uma força vertical no pedal do dispositivo é necessária para produzir uma força trativa de na barra de controle vertical. Determine as reações correspondentes nos mancais em e .
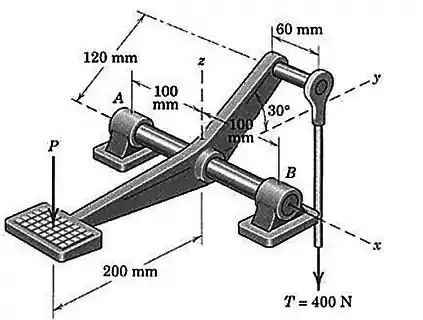
Passo 1
O diagrama de corpo livre fica assim:
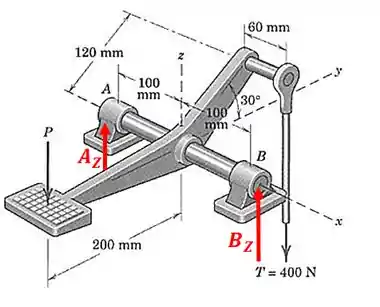
Passo 2
Vamos começar calculando o momento em relação ao eixo :
Repare que a distância da força até o eixo é:
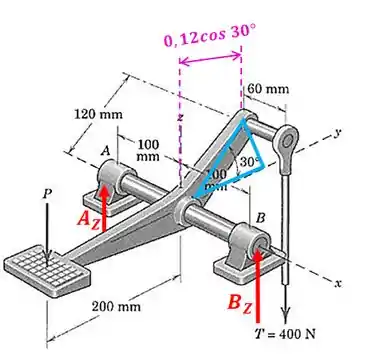
Então:
Passo 3
Agora vamos fazer o somatório de momentos com relação a uma reta que passe pelo ponto e que seja paralela ao eixo :
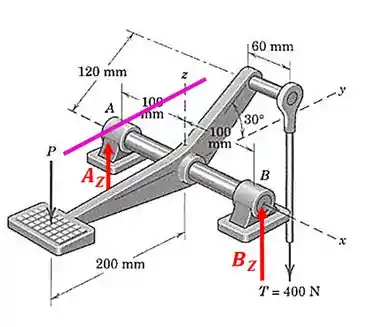
Então:
Passo 4
Para achar as reações de apoio, vamos fazer o somatório das forças:
Como não há nenhuma força no eixo , então não vai ter reações neste eixo nos apoios em e .
Resposta
Exercícios de Livros Relacionados
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B ea tração no membro E D . A força agindo em D é F = 135 i ^
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B e a tração no membro E D . A força agindo em D é F = 135 i
Uma placa circular horizontal de peso igual a 267 N é suspensa por três fios que são ligados a um suporte D e formam ângulos de 30° com a vertical. Determine a tração em cada fio.
Por que as equações escalares de equilíbrio da estática no espaço tridimensional são em número de seis? Mais do que três equações de momento nulo podem ser consideradas nessa equação? Como e por quê?
Determine as forças trativas nos cabos A B , A C e A D .