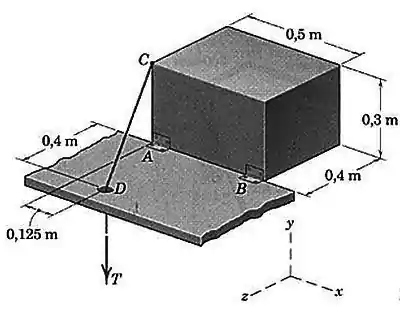
Determine a força trativa necessária para manter o sólido retangular na posição mostrada. O sólido retangular com é homogêneo. O atrito em é desprezível.
Passo 1
O diagrama de corpo livre do sólido fica assim:
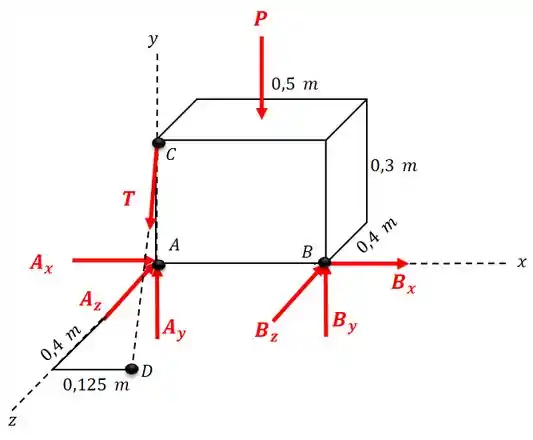
Passo 2
Vamos calcular o módulo da força peso do sólido:
E a foça trativa ? Temos que calcular a sua direção e sentido que é dada pela reta que vai do ponto em direção ao ponto :
Temos que as coordenadas dos pontos e são:
E:
Então:
Então, o vetor normalizado fica:
Então, a força trativa fica:
Passo 3
Vamos começar calculando o momento em relação à reta que esta no eixo , pois as incógnitas de reação de apoio dos pontos e não terão braço de alavanca com relação a este eixo:
Perceba que somente a componente da força trativa terá braço de alavanca com relação à reta , pois a componente é paralela a esta reta e a componente tem sua linha de ação cruzando a reta .
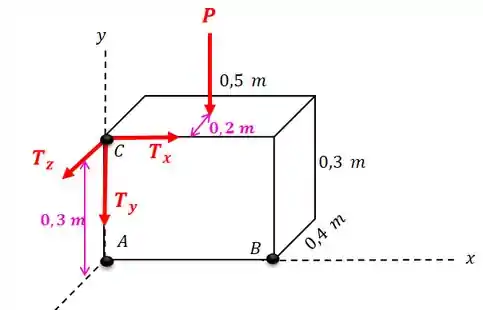
Então: