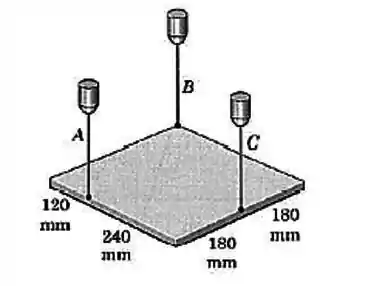
Uma chapa quadrada e uniforme de aço de de comprimento de aresta e uma massa de está suspensa no plano horizontal pelos três fios verticais, como mostrado. Calcule a força trativa de cada fio.
Passo 1
Vamos desenhar o sistema junto com os eixos:
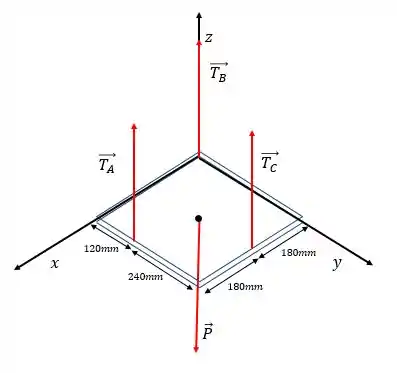
Para que a placa esteja em equilíbrio, as seguintes relações precisam ser satisfeitas:
Passo 2
Vamos primeiro calcular os momentos em relação ao eixo
Para isso, perceba que e tendem a girar a placa em torno do eixo no mesmo sentido; já o peso, tende a girar a placa no sentido contrário. Além disso, perceba que está a uma distância de do eixo , a uma distância de e a uma distância de
Sendo, o módulo da força peso da placa igual a:
Então, os momentos de cada uma das forças com relação ao eixo é::
Como todos os termos estão multiplicados por , podemos cortar ele da equação:
Dividindo tudo por
E perceba que não realiza momento, pois ele está bem em cima do eixo e não tem braço de alavanca com relação a este eixo.
Passo 3
Agora vamos para o eixo
Aqui as forças e continuam exercendo momento de sentidos iguais assim como o momento do peso continua se opondo a eles. O que mudou foi a distância das forças:
está a uma distância de do eixo , e está a uma distância de do eixo. tem uma distância de do eixo:
Cortando todos os
Passo 4
Já temos esse sistema aqui:
Podemos subtrair a primeira equação da segunda:
Substituindo essa relação na segunda equação:
E será:
Passo 5
Agora, para achar , basta a agente usar a relação do equilíbrio das forças:
Assim: