O mastro de , com centro de massa em , é mantido na posição mostrada por uma rótula em e por dois cabos e . Determine as forças trativas nos dois cabos e as componentes , e da força de reação em .
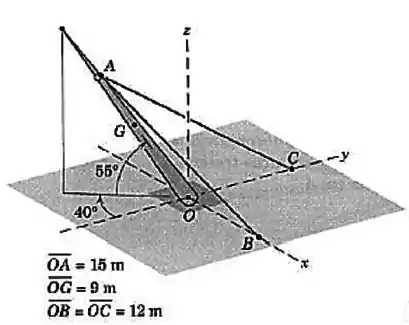
Passo 1
O sistema acima pode ser representado pelo desenho abaixo:
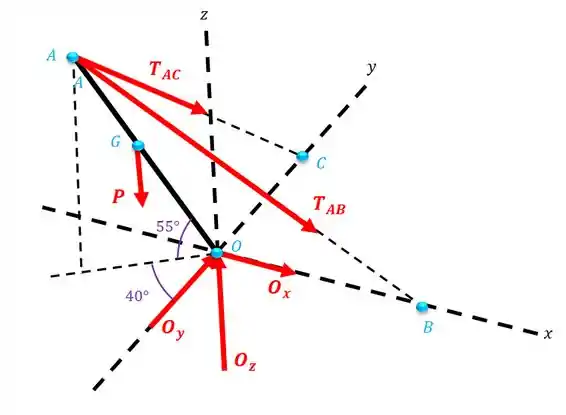
Passo 2
Vamos escrever cada uma das forças na forma vetorial:
Coordenadas do ponto :
Temos uma coordenada no eixo
Pra achar as coordenadas , basta projetar na horizontal e depois projetar em cada um dos eixos, e
Assim:
E as coordenadas do centro de gravidade (onde o peso é aplicado)?
Assim:
As coordenadas de são:
E de
Passo 3
Assim:
Então:
E:
O peso é dado por:
E ainda temos as forças de reação em
Passo 4
Vamos aplicar as equações de equilíbrio de forças:
Percebam que temos 3 equações e 5 incógnitas ! Precisamos de mais 2 equações para determinar todas as incógnitas.
Acho que chegou o Momento de perguntar quais são essas 2 equações, certo? Vamos trabalhar com o equilíbrio de momentos na direção na direção do eixo :
E:
Resolvendo o sistema de equações acima: