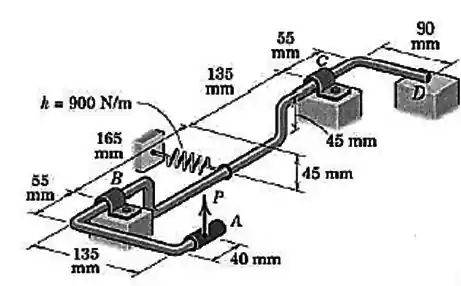
A mola de módulo é esticada de uma distância quando o mecanismo está na posição mostrada. Calcule a força necessária para iniciar rotação em torno do eixo e determine os módulos correspondentes das forças nos mancais, as quais são perpendiculares à . Qual é a força de reação normal em se ?
Passo 1
O desenho abaixo pode exemplificar o sistema:
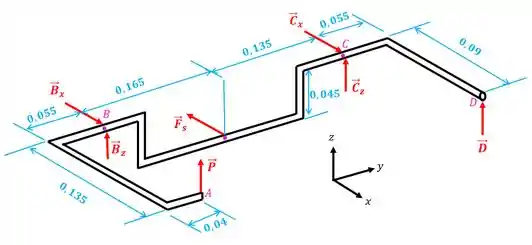
Perceba que é a força elástica.
Passo 2
O módulo da força elástica é dado por:
Na situação de rotação, a reação vai ser nula: Para esse caso, vamos calcular as reações:
Com relação ao eixo :
E:
Passo 3
Pelo equilíbrio de forças:
E no eixo :
Assim, os módulos serão:
Passo 4
Para o caso em que :
Assim, nesse caso, a força será:
Resposta
Exercícios de Livros Relacionados
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B ea tração no membro E D . A força agindo em D é F = 135 i ^
A estrutura de três membros é conectada em suas extremidades por meio de juntas esféricas. Determine as componentes x , y , z da reação em B e a tração no membro E D . A força agindo em D é F = 135 i
Uma placa circular horizontal de peso igual a 267 N é suspensa por três fios que são ligados a um suporte D e formam ângulos de 30° com a vertical. Determine a tração em cada fio.
Por que as equações escalares de equilíbrio da estática no espaço tridimensional são em número de seis? Mais do que três equações de momento nulo podem ser consideradas nessa equação? Como e por quê?
Determine as forças trativas nos cabos A B , A C e A D .