A placa possui um peso com centro de gravidade em . Determine a tração desenvolvida nos fios , e se a força é aplicada em .
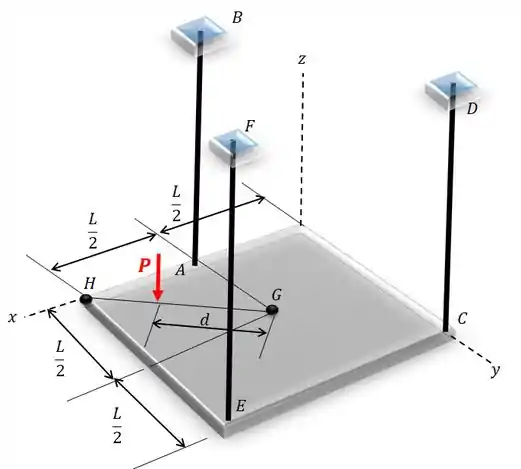
Passo 1
O diagrama de corpo livre fica assim:
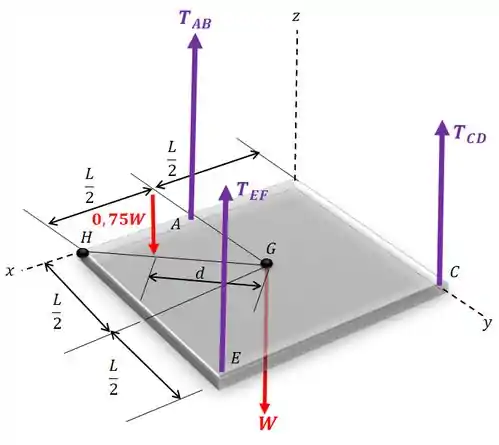
Passo 2
Vamos começar calculando o somatório de momentos com relação a reta que liga os pontos e :
Com isso, ficamos com apenas uma incógnita que é a força trativa .
Mas antes temos que descobrir a distância da força até a reta . Para isso vamos fazer semelhança de triângulos:
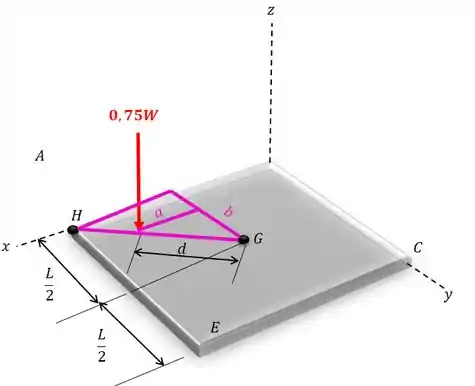
Temos que:
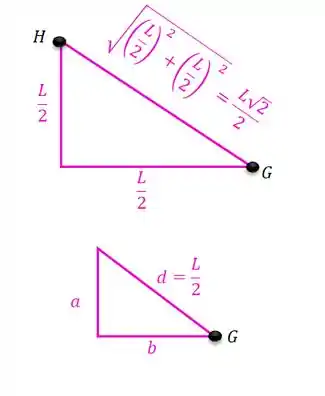
Repare que para achar a hipotenusa do triângulo maior foi feito Teorema de Pitágoras!
Para achar o lado do triângulo menor, temos que:
Sabendo que , temos que:
E o lado será igual ao lado , pois:
Passo 3
Agora sim podemos calcular o momento com relação a reta que liga os ponto e . Sabendo que os braços de alavanca são:
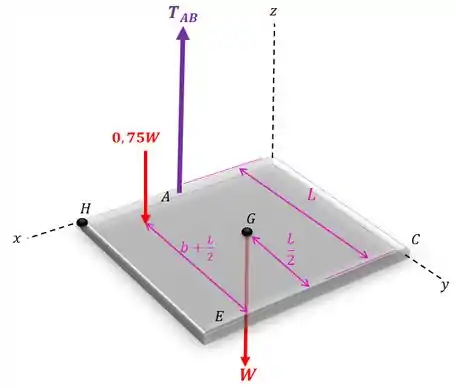
Então:
Podemos cortar o de todos os termos:
Passo 4
Agora vamos fazer o momento com relação ao eixo :
Para isso vamos ter os seguintes braços de alavanca:
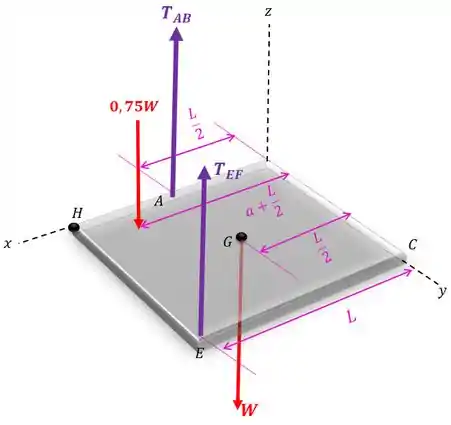
Novamente podemos cortar o de todos os termos:
Passo 5
Para finalizar, vamos fazer o equilíbrio de forças verticais: